湖南省长沙市周南教育集团2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-10-10 类型:期中考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , ,则 的值是( )A、2 B、6 C、8 D、164. 若 中不含x项,那么a的值为( )A、0 B、2 C、-2 D、45. 已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( )A、AB=DE,AC=DF B、AC=EF,BC=DF C、AB=DE,BC=EF D、∠C=∠F,BC=EF6. 下图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=8m,∠A=30°,则立柱BC的长度为( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 已知 , ,则 的值是( )A、2 B、6 C、8 D、164. 若 中不含x项,那么a的值为( )A、0 B、2 C、-2 D、45. 已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( )A、AB=DE,AC=DF B、AC=EF,BC=DF C、AB=DE,BC=EF D、∠C=∠F,BC=EF6. 下图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=8m,∠A=30°,则立柱BC的长度为( ) A、4m B、8m C、10m D、16m7. 如图,在△ABC中,AB=10,AC=6,BC的垂直平分线交AB于D,交BC于E,则△ADC的周长等于( )
A、4m B、8m C、10m D、16m7. 如图,在△ABC中,AB=10,AC=6,BC的垂直平分线交AB于D,交BC于E,则△ADC的周长等于( )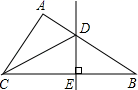 A、4 B、6 C、10 D、168. 如图,将一个长方形 纸片沿着 折叠,使 两点分别落在点 处.若 ,则 的度数为( )
A、4 B、6 C、10 D、168. 如图,将一个长方形 纸片沿着 折叠,使 两点分别落在点 处.若 ,则 的度数为( )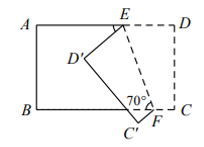 A、70° B、40° C、30° D、20°9. 如图,在已知的△ABC中,按以下步骤作图:
A、70° B、40° C、30° D、20°9. 如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
 A、50° B、45° C、30° D、25°10. 从边长为 的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A、50° B、45° C、30° D、25°10. 从边长为 的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( ) A、 B、 C、 D、11. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )
A、 B、 C、 D、11. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )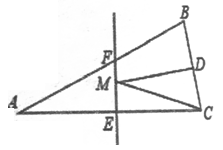 A、6 B、8 C、10 D、1212. 已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( )
A、6 B、8 C、10 D、1212. 已知,如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下列结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP;其中正确的序号是( ) A、①③④ B、②③ C、①②④ D、①③
A、①③④ B、②③ C、①②④ D、①③二、填空题
-
13. 若点A(a,﹣2)与点B(﹣3,b)关于x轴对称,则ab= .14. 等腰三角形的两边长分别为3和4,则周长为.15. 若 是关于 的完全平方式,则m的值是 .16. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6,那么CE= .
 17. 如图,某居民小区有一块长为 (3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一个雕塑,底座是边长为(a+b)米的正方形.绿化的面积是多少平方米 .
17. 如图,某居民小区有一块长为 (3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一个雕塑,底座是边长为(a+b)米的正方形.绿化的面积是多少平方米 . 18. 已知x≠1,计算:(1﹣x)(1+x)=1﹣x2 , (1﹣x)(1+x+x2)=1﹣x3 .(1)、观察以上各式并猜想:(1﹣x)(1+x+x2+……+xn)=(n为正整数).(2)、根据你的猜想计算:
18. 已知x≠1,计算:(1﹣x)(1+x)=1﹣x2 , (1﹣x)(1+x+x2)=1﹣x3 .(1)、观察以上各式并猜想:(1﹣x)(1+x+x2+……+xn)=(n为正整数).(2)、根据你的猜想计算:①(1﹣2)(1+2+22+23+24+25)=;
②2+22+23+…+2n=(n为正整数).
三、解答题
-
19. 计算:(1)、 .(2)、20. 利用乘法公式计算:(1)、(2x﹣3y)2﹣(y+3x)(3x﹣y)(2)、(a﹣2b+3)(a+2b﹣3).21. 已知x+y=7,xy=2,求下列各式的值:(1)、x2+y2;(2)、2(x﹣y)2 .22. 先化简,再求值:(2+a)(2﹣a)+a(a﹣5b)+3a5b3÷(﹣a2b)2 , 其中ab=﹣2.23. 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1 , 并求出△ABC的面积.
 24. 如图,△AOB,△COD是等腰直角三角形,点D在AB上.
24. 如图,△AOB,△COD是等腰直角三角形,点D在AB上.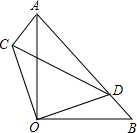 (1)、求证:△ACO≌△BDO;(2)、若∠BOD=30°,求∠ACD度数.25. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
(1)、求证:△ACO≌△BDO;(2)、若∠BOD=30°,求∠ACD度数.25. 如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,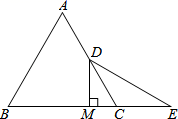 (1)、求证:M是BE的中点.(2)、若CD=1,DE= ,求△ABD的周长.26. 中, ,直线 过点 .(1)、当 时,如图1,分别过点 和 作 直线 于点 直线 于点 与 是否全等,并说明理由;
(1)、求证:M是BE的中点.(2)、若CD=1,DE= ,求△ABD的周长.26. 中, ,直线 过点 .(1)、当 时,如图1,分别过点 和 作 直线 于点 直线 于点 与 是否全等,并说明理由;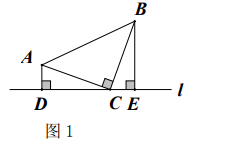 (2)、当 时,如图2,点 与点 关于直线 对称,连接 点 在 上,点 是 上一点,分别过点 作 直线 于点 直线 于点 ,点 从点 出发,以每秒 的速度沿 路径运动,终点为 点 从点 出发,以每秒 的速度沿 路径运动,终点为 ,点 同时开始运动,各自达到相应的终点时停止运动,设运动时间为 秒.
(2)、当 时,如图2,点 与点 关于直线 对称,连接 点 在 上,点 是 上一点,分别过点 作 直线 于点 直线 于点 ,点 从点 出发,以每秒 的速度沿 路径运动,终点为 点 从点 出发,以每秒 的速度沿 路径运动,终点为 ,点 同时开始运动,各自达到相应的终点时停止运动,设运动时间为 秒.
①当 为等腰直角三角形时,求 的值;
②当 与 全等时,求 的值.
27. 如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣ |=0. (1)、求A点和D点的坐标;(2)、若∠DAE= ∠OAB,请猜想DE,OD和EB的数量关系,说明理由.(3)、若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.
(1)、求A点和D点的坐标;(2)、若∠DAE= ∠OAB,请猜想DE,OD和EB的数量关系,说明理由.(3)、若∠OAD=30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明.