湖南省长沙市长郡教育集团2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-10-10 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 等式(x+4)0=1成立的条件是( )
2. 等式(x+4)0=1成立的条件是( )
A、x为有理数 B、x≠0 C、x≠4 D、x≠-43. 下列运算中,正确的是( )A、 B、 C、 D、4. 若(2a+3b)( )=4a2﹣9b2 , 则括号内应填的代数式是( )A、﹣2a﹣3b B、2a+3b C、2a﹣3b D、3b﹣2a5. 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( ) A、15° B、30° C、45° D、60°6. 下列各式中,能用完全平方公式计算的是( )A、(a﹣b)(﹣b﹣a) B、(﹣n2﹣m2)(m2+n2) C、 D、(2x﹣3y)(2x+3y)7. 下列说法错误的是( )A、关于某条直线对称的两个三角形一定全等 B、轴对称图形至少有一条对称轴 C、全等三角形一定能关于某条直线对称 D、角是轴对称的图形8.
A、15° B、30° C、45° D、60°6. 下列各式中,能用完全平方公式计算的是( )A、(a﹣b)(﹣b﹣a) B、(﹣n2﹣m2)(m2+n2) C、 D、(2x﹣3y)(2x+3y)7. 下列说法错误的是( )A、关于某条直线对称的两个三角形一定全等 B、轴对称图形至少有一条对称轴 C、全等三角形一定能关于某条直线对称 D、角是轴对称的图形8.如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
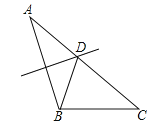 A、8 B、9 C、10 D、119. 如果x2﹣(m+1)x+1是完全平方式,则m的值为( )A、﹣1 B、1 C、1或﹣1 D、1或﹣310. 下列各式成立的是( )A、 =1 B、(﹣a﹣b)2=(a+b)2 C、(a﹣b)2=a2﹣b2 D、(a+b)2﹣(a﹣b)2=2ab11. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE , ∠A=40°,则∠CDE的度数为( )
A、8 B、9 C、10 D、119. 如果x2﹣(m+1)x+1是完全平方式,则m的值为( )A、﹣1 B、1 C、1或﹣1 D、1或﹣310. 下列各式成立的是( )A、 =1 B、(﹣a﹣b)2=(a+b)2 C、(a﹣b)2=a2﹣b2 D、(a+b)2﹣(a﹣b)2=2ab11. 如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE , ∠A=40°,则∠CDE的度数为( ) A、50° B、40° C、60° D、80°12. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )
A、50° B、40° C、60° D、80°12. 如图,在 中, 面积是16, 的垂直平分线 分别交 边于 点,若点 为 边的中点,点 为线段 上一动点,则 周长的最小值为( )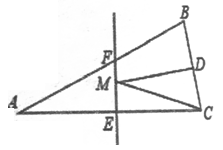 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题
-
13. 分解因式: .14. 若(x+p)与(x+5)的乘积中不含x的一次项,则p= .15. 如图,AB=AC=8cm,DB=DC,若∠ABC=60°,则BE=cm.
 16. 若(a-b)2=4,ab= ,则(a+b)2=.17. 如图,在 中, , , 平分 ,交 于点 ,若 ,则 .
16. 若(a-b)2=4,ab= ,则(a+b)2=.17. 如图,在 中, , , 平分 ,交 于点 ,若 ,则 . 18. 如图,在 中, ,点 在 延长线上, 于点 ,交 于点 ,若 , ,则 的长度为 .
18. 如图,在 中, ,点 在 延长线上, 于点 ,交 于点 ,若 , ,则 的长度为 .
三、解答题
-
19. 计算:(1)、﹣12x2y3÷(﹣3xy2)•(﹣ xy)(2)、3a2(a3b2﹣2a)﹣4a(﹣a2b)220. 因式分解:(1)、x2﹣4x﹣12(2)、a3﹣4a2+4a21. 运用乘法公式计算:(1)、98×102(2)、(2x﹣3y)2+(x﹣2y)(x+2y)22. 先化简,再求值 ,其中x= .23. 如图,在平面直角坐标系 中, , , .
 (1)、在图中作出 关于 轴的对称图形 ;(2)、写出点 , , 的坐标(直接写答案). . , .(3)、求 的面积.24. 如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)、在图中作出 关于 轴的对称图形 ;(2)、写出点 , , 的坐标(直接写答案). . , .(3)、求 的面积.24. 如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.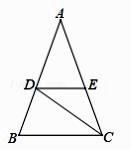 (1)、求证:DE=CE.(2)、若∠CDE=35°,求∠A 的度数.25. 如图,点 , , 分别在等边 的各边上,且 于点 , 于点 , 于点 .
(1)、求证:DE=CE.(2)、若∠CDE=35°,求∠A 的度数.25. 如图,点 , , 分别在等边 的各边上,且 于点 , 于点 , 于点 . (1)、求证: 是等边三角形;(2)、若 ,求 的长.26. 如图, 中, ,现有两点 、 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s , 点N的速度为2 cm/s.当点N第一次到达B点时, 、 同时停止运动.
(1)、求证: 是等边三角形;(2)、若 ,求 的长.26. 如图, 中, ,现有两点 、 分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s , 点N的速度为2 cm/s.当点N第一次到达B点时, 、 同时停止运动. (1)、点 、 运动几秒时, 、 两点重合?(2)、点 、 运动几秒时,可得到等边三角形 ?(3)、当点 、 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时 、 运动的时间.27. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)、点 、 运动几秒时, 、 两点重合?(2)、点 、 运动几秒时,可得到等边三角形 ?(3)、当点 、 在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时 、 运动的时间.27. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.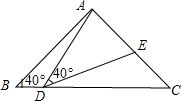 (1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.