湖南省岳阳市临湘市2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-10-10 类型：期中考试
一、单选题
-
1. 已知 、 为 的两个锐角， ，则 的度数为（ ）A、 B、 C、 D、2. 在直角三角形中，若勾为3，股为4，则弦为（ ）A、5 B、6 C、7 D、83. 如图，AC＝BC，AC⊥OA，CB⊥OB，则 Rt△AOC≌Rt△BOC 的理由是（ ）
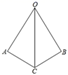A、SSS B、ASA C、SAS D、HL4. 如图所示，在 中， ， 平分 ， ， ，则点 到 的距离为（ ）
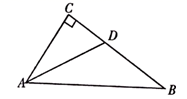A、18 B、12 C、15 D、无法确定5. 如果一个多边形的内角和与外角和相等，那么这个多边形是（ ）A、四边形 B、五边形 C、六边形 D、七边形6. 如图，在平行四边形 中， ，点 ， 分别是 ， 的中点，则 等于（ ）
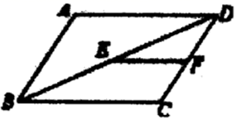A、2 B、3 C、4 D、57. 下列说法正确的是（ ）A、平行四边形的对角线互相平分且相等 B、矩形的对角线相等且互相平分 C、菱形的对角线互相垂直且相等 D、正方形的对称轴是正方形的对角线8.如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH=（ ）
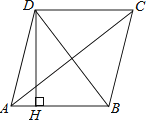A、 B、 C、12 D、24二、填空题
-
9. 在 中，若 与 互余，则 是三角形．10. 如图：在 中，CD是斜边AB上的中线，若 ，则 ．
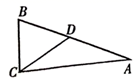11. 直角三角形的直角边长分别为5，12，斜边长为 ，则 ．12. 如图，∠AOB=60°，CD⊥OA于D，CE⊥OB于E，且CD=CE，则∠DOC=
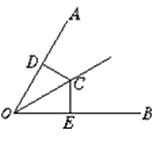13. 七边形的内角和是14. 王明、杨磊两家所在位置关于学校成中心对称，如果王明距学校500米，那么他们两家相距米．15. 如图，在平行四边形 中， ， ， ，则 .
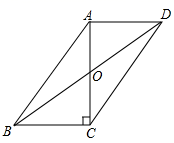16. 矩形纸片ABCD中，AD=10cm，AB=4cm，按如图方式折叠，使点D与点B重合，折叠为EF，则DE=cm.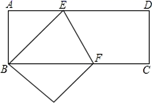
三、解答题
-
17. 如图，在 中，已知 ， ．
(1)、求证： 为直角三角形；(2)、求 边上的中线长．18. 如图，在 中， ， 为 的中点， ， ，垂足分别 、 ，求证： ．
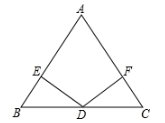19. 如图，在 ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，求证：AE=CF.
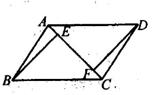20. 如图，在四边形 中， ， 的面积为 ， ， ， ．
(1)、试判断 的形状；(2)、求 的面积．21. 如图， 与 关于O点中心对称，点E、F在线段AC上，且AF=CE．求证：FD=BE．
22. 如图，在正方形ABCD中，AF=BE ， AE与DF相交于于点O ．
(1)、求证：△DAF≌△ABE；(2)、求∠AOD的度数．23. 如图，在▱ABCD中，AE⊥BC于点E点，延长BC至F点使CF=BE，连接AF，DE，DF．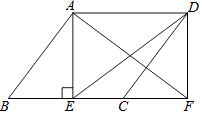
(1)、求证：四边形AEFD是矩形；(2)、若AB=6，DE=8，BF=10，求AE的长．24. 如图，在 中， ， ， ，点 从点 出发沿 方向以每秒2个单位长度的速度向点 运动，同时点 从点 出发沿 方向以每秒1个单位长度的速度向点 运动，当其中一个点到达终点时，另一个点也随之停止运动，设点 ， 运动的时间是 秒( )．过点 作 于点 ，连接 、 ．
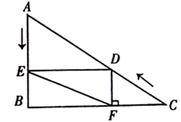(1)、求 、 的长；(2)、求证： ；(3)、四边形 能够成为菱形吗？如果能，求出相应的 值；如果不能，说明理由．