湖南省永州市蓝山县2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-10-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列代数式中，分式有______个
$\frac{3}{x}$ ， $\frac{x}{3}$ ， $\frac{a - 1}{a}$ ， $- \frac{3}{5 + y}$ ， $\frac{2 x}{x - y}$ ， $\frac{m - n}{2}$ ， $\frac{x}{2} + 3$ ， $\frac{x + y}{π}$ ，

A、5 B、4 C、3 D、2

查看试题解析
2. 要使分式 $\frac{1}{x + 2}$ 有意义，则x的取值应满足（　　）

A、x=﹣2 B、x≠2 C、x＞﹣2 D、x≠﹣2

查看试题解析
3. 若把分式 $\frac{x y}{x + y}$ 的x和y都扩大5倍，则分式的值（）

A、扩大到原来的5倍 B、不变 C、缩小为原来的 $\frac{1}{5}$ 倍 D、扩大到原来的25倍

查看试题解析
4. 下列运算错误的是（）

A、 ${(- \frac{a}{b})}^{2} = \frac{a^{2}}{b^{2}}$ B、 $- {(2^{n})}^{2} = 2^{2 n}$ C、 $- a^{2} b^{2} \cdot 3 a b^{3} = - 3 a^{3} b^{5}$ D、 $x^{2} \times x^{5} \times x^{- 7} = 1$

查看试题解析
5. 九年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.设骑车学生的速度为x km/h，则所列方程正确的是（）

A、 $\frac{10}{x} = \frac{10}{2 x} - \frac{1}{3}$ B、 $\frac{10}{x} = \frac{10}{2 x} - 20$ C、 $\frac{10}{x} = \frac{10}{2 x} + \frac{1}{3}$ D、 $\frac{10}{x} = \frac{10}{2 x} + 20$

查看试题解析
6. 下列分式是最简分式的是（）

A、 $\frac{a + b}{a^{2} + b^{2}}$ B、 $- \frac{m^{2}}{m n^{3}}$ C、 $- \frac{x^{2} - 9 y^{2}}{x^{2} - 6 x y + 9 y^{2}}$ D、 $\frac{x^{2} - 4}{x + 2}$

查看试题解析
7. 以下列长度为边的三根木棒能首尾相接构成一个三角形的是（）

A、2cm、3cm、6cm B、2cm、3cm、5cm C、2cm、3cm、4cm D、8cm、3cm、4cm

查看试题解析
8. 下列说法：①若直线PE是线段AB的垂直平分线，则EA=EB，PA=PB；②若PA=PB，EA=EB，则直线PE垂直平分线段AB；③若PA=PB，则点P必是线段AB的垂直平分线上的点；④若EA=EB，则过点E的直线垂直平分线段AB．其中正确的个数有（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析
9. 下列图形中AD是三角形ABC的高线的是（）

A、 B、 C、 D、

查看试题解析
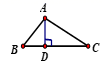10. 如图：若AD=AE，要证明△ABE≌△ACD，添加下列条件还不能证明的是（）

A、AC＝AB B、∠B=∠C C、BE=CD D、∠BDC=∠CEB

查看试题解析

二、填空题

11. 分式 $\frac{1}{a + b}$ ， $\frac{b}{2 a - 2 b}$ ， $\frac{a}{a^{2} - b^{2}}$ 的最简公分母是．

查看试题解析
12. 我国新修订的《环境空气质量标准》中增加了PM2.5检测指标，“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物，2.5微米即0.0000025米．数0.0000025用科学记数法表示为．

查看试题解析
13. 计算 ${(\frac{x}{- y})}^{2} \cdot {(\frac{y^{2}}{x})}^{3} \div {(\frac{y}{x})}^{4}$ 的结果是．

查看试题解析
14. “对顶角相等”的逆命题是命题（填真或假）

查看试题解析
15. 证明命题“直角三角形中的两个锐角中至少有一个角不小于45°”时，如果用反证法证明，应先假设．

查看试题解析
16. 在△ABC中，若∠A：∠B：∠C=2：3：4，则∠A、∠B、∠C的外角的比是．

查看试题解析
17. 等腰三角形的一个外角是60°，则这个三角形的底角等于°．

查看试题解析
18. 已知： $2^{m} = 12$ ， $2^{n} = 48$ ，试计算： ${(- 3)}^{m - n}$ = ．

查看试题解析

三、解答题

19. 计算

(1)、 $\frac{2 x + y}{x^{2} - y^{2}} - \frac{3 y}{x^{2} - y^{2}}$

(2)、 $\frac{1}{x + 3} + \frac{6}{x^{2} - 9}$

查看试题解析
20. 先化简，再求值： $\frac{{(a - b)}^{3}}{a b} \div {(a - b)}^{2} • {(\frac{a b}{a - b})}^{2}$ ，其中 $a = 1, b = 2$ ．

查看试题解析
21. 解方程：

(1)、 $\frac{3}{x + 1} = \frac{5}{x + 3}$

(2)、若分式方程： $\frac{3}{x - 2} = \frac{a}{x} + \frac{4}{x (x - 2)}$ 无解，求a的值．

查看试题解析
22. 如图，A、B、C三个居民小区，现要建一个生活超市，使它到这三个居民小区的距离相等，试确定生活超市位置P．

查看试题解析
23. 如图，点A、 $B$ 、 $C$ 、 $D$ 在同一直线上， $A F = D E$ ，AF∥DE， $A C = D B$ .求证： $Δ A B F ≌ Δ D C E$ .

查看试题解析
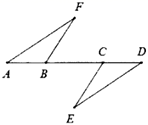24. 某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1.5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．

(1)、这项工程的规定时间是多少天？

(2)、已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？

查看试题解析
25. 如图，点O是等边三角形ABC内一点，∠AOB=110°，∠BOC=β．将△BOC绕点C按顺时针方向旋转60°得到△ADC，连接OD．

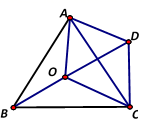(1)、求证：△COD是等边三角形；

(2)、当β=150°时，试判断△AOD的形状，并说明理由；

(3)、探究：当β为多少度时，△AOD是以OD为底边的等腰三角形？

查看试题解析
26. 阅读：材料1：只含有一个未知数，并且未知数的最高次数是2次，最高次项的系数不为零，这样的整式方程叫做一元二次方程.一元二次方程有一种解法是利用因式分解来解的.如解方程：x²﹣3x+2＝0，左边分解因式得（x﹣1）（x﹣2）＝0，所以x﹣1＝0或x﹣2＝0，所以原方程的解是x＝1或x＝2.
材料2：立方和公式用字母表示为：x³+y³＝（x+y）（x²﹣xy+y²），

(1)、请利用材料1的方法解方程：x²﹣4x+3＝0；

(2)、请根据材料2类比写出立方差公式：x³﹣y³＝；（提示：可以用换元方法）

(3)、结合材料1和2，请你写出方程x⁶﹣7x³﹣8＝0所有根中的两个根.

查看试题解析