湖南省益阳市南县2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-10-10 类型:期中考试
一、单选题
-
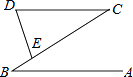
1. 要使分式 有意义, 的取值范围是 ( )A、 B、 C、 D、2. 把0.00025用科学记数法表示出来,正确的是( )A、 B、 C、 D、3. 计算 的结果为( )A、 B、 C、 D、4. 计算 的结果为( )A、 B、-2 C、 D、165. 已知A、C两地相距40千米,B、C两地相距50千米,甲乙两车分别从A、B两地同时出发到C地.若乙车每小时比甲车多行驶12千米,则两车同时到达C地.设乙车的速度为x千米/小时,依题意列方程正确的是( )A、 B、 C、 D、6. 已知等腰△ABC的两边长分别为2和3,则等腰△ABC的周长为( )A、7 B、8 C、6或8 D、7或87. 等腰三角形的一个角是80°,则它的顶角的度数是( )A、80° B、80°或20° C、80°或50° D、20°8. 如图,AB∥CD,点E在BC上,且CD=CE,∠D=74°,则∠B的度数为( )
 A、68° B、32° C、22° D、16°
A、68° B、32° C、22° D、16°二、填空题
-
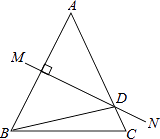
9. 若 ,则 = .10. 若代数式 和 的值相等,则x= .11. 如果关于 的方程 有增根,则 .12. 如图,等腰△ABC中,AB=AC,∠DBC=15°,AB的垂直平分线MN交AC于点D,则∠A的度数是 .
 13. 如图,△ABC中,AB=AC,点D,E在BC边上,当 时,△ABD≌△ACE.(添加一个适当的条件即可)
13. 如图,△ABC中,AB=AC,点D,E在BC边上,当 时,△ABD≌△ACE.(添加一个适当的条件即可) 14. 观察下列一组数: , , , , ,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
14. 观察下列一组数: , , , , ,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
三、解答题
-
15. 填写下列证明过程中的推理根据:
已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分于∠ABO与AC相交于E,∠A=∠C.求证:∠1=∠2.

证明:∵∠A=∠C( ▲ ),
∴AB∥CD ( ▲ ),
∴∠ABO=∠CDO ( ▲ ),
又∵∠1= CDO,∠2= ∠ABO ( ▲ ),
∴∠1=∠2( ▲ ).
16. 计算:17. 先化简,再求值: ,在﹣2,0,1,2四个数中选一个合适的代入求值.18. 国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获补贴500元.若同样用11万元所购买此款空调,补贴后可购买的台数比补贴前多20%,则该款空调补贴前的售价为每台多少元?
19. 如图,在等边三角形ABC中,D是BC边的中点,E是AB延长线上的一点,且BE=BD. (1)、求∠BAD和∠BDE的度数;(2)、求证:AD=DE.
(1)、求∠BAD和∠BDE的度数;(2)、求证:AD=DE.