初中数学苏科版八年级上册3.1 勾股定理 同步练习
试卷更新日期:2020-10-10 类型:同步测试
一、单选题
-
1. 在△ABC,∠A,∠B,∠C的对应边分别是a,b,c,若∠B=90°,则下列等式中成立的是( )A、a2+b2=c2 B、b2+c2=a2 C、 a2+c2=b2 D、c2- a2= b22. 下列各组数中,不是勾股数的为( )A、3,4,5 B、6,8,10 C、5,12,13 D、5,7,103. 三个正方形的面积如图所示,则面积为 的正方形的边长为( )
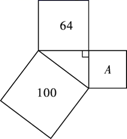 A、164 B、36 C、8 D、64. 如图,图中的四边形都是正方形,三角形都是直角三角形,其中正方形的面积分别记为A,B,C,D,则它们之间的关系为( )
A、164 B、36 C、8 D、64. 如图,图中的四边形都是正方形,三角形都是直角三角形,其中正方形的面积分别记为A,B,C,D,则它们之间的关系为( ) A、A+B=C+D B、A+C=B+D C、A+D=B+C D、以上都不对5. 如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
A、A+B=C+D B、A+C=B+D C、A+D=B+C D、以上都不对5. 如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )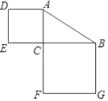 A、16 B、32 C、160 D、2566. 如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A、16 B、32 C、160 D、2566. 如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )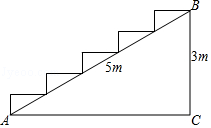 A、4米 B、5米 C、6米 D、7米7. 若直角三角形的三边长分别为2、4、x,则x的可能值有( )
A、4米 B、5米 C、6米 D、7米7. 若直角三角形的三边长分别为2、4、x,则x的可能值有( )
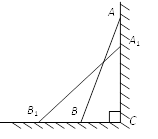
A、1个 B、2个 C、3个 D、4个 8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( ) A、0.7米 B、1.5米 C、2.2米 D、2.4米9. 如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )
A、0.7米 B、1.5米 C、2.2米 D、2.4米9. 如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )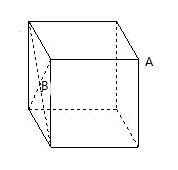 A、9 B、 C、 D、1210. 将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( )
A、9 B、 C、 D、1210. 将一根长24cm的筷子置于底面直径为5cm,高为12cm的圆柱水杯中,设筷子露在杯子外面的长度为h,则h的取值范围是( )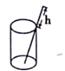 A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm
A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm二、填空题
-
11. 如果一个直角三角形两直角边长分别为3和4,斜边长是 .12. 已知直角三角形的两直角边长分别为3和5,则第三边的长是 .13. 如图,则阴影小长方形的面积S= .
 14. 甲、乙两人同时从同一地点出发,甲往东走了8km,乙往南走了6km,这时两人相距km.15. 在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .16. 若直角三角形的两条边长为a,b,且满足(a﹣3)2+|b﹣4|=0,则该直角三角形的第三条边长为 .17. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为 .
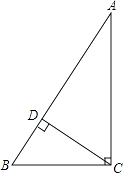
14. 甲、乙两人同时从同一地点出发,甲往东走了8km,乙往南走了6km,这时两人相距km.15. 在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .16. 若直角三角形的两条边长为a,b,且满足(a﹣3)2+|b﹣4|=0,则该直角三角形的第三条边长为 .17. 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为 . 18. 如图所示,是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位: )则两圆孔中心 和 的距离是 .
18. 如图所示,是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位: )则两圆孔中心 和 的距离是 .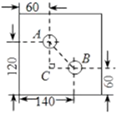 19. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
19. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .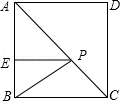 20. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为米.
20. 如图,在一次测绘活动中,某同学站在点A的位置观测停放于B、C两处的小船,测得船B在点A北偏东75°方向900米处,船C在点A南偏东15°方向1200米处,则船B与船C之间的距离为米.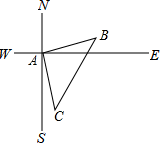
三、综合题
-
21. 在Rt△ABC中,∠C=90°(1)、已知a=6, c=10,求b,(2)、已知a=40,b=9,求c;(3)、已知c=25,b=15,求a.