辽宁省大连市甘井子区2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入出卷网下载

一、选择题

1. 将一元二次方程5x²﹣1＝4x化为一般形式，其中一次项系数是（）

A、5 B、﹣4 C、4 D、﹣1

查看试题解析
2. 下列图形中，不是中心对称图形的是（）

A、平行四边形 B、圆 C、等边三角形 D、正六边形

查看试题解析
3. 如图，四边形ABCD和四边形EFGH相似，则下列角的度数正确的是（）

A、∠D＝81° B、∠F＝83° C、∠G＝78° D、∠H＝91°

查看试题解析
4. 将抛物线 $y = \frac{1}{2} {(x + 2)}^{2} - 2$ 向右平移3个单位长度，再向上平移3个单位长度，所得的抛物线解析式为（）

A、 $y = \frac{1}{2} {(x + 5)}^{2} - 5$ B、 $y = \frac{1}{2} {(x + 5)}^{2} +1$ C、 $y = \frac{1}{2} {(x - 1)}^{2} - 5$ D、 $y = \frac{1}{2} {(x - 1)}^{2} + 1$

查看试题解析
5. 已知点A(a，1)与点B(5，b)关于原点对称，则a、b值分别是（）

A、a=5，b=1 B、a=﹣5，b=1 C、a=﹣5，b=﹣1 D、a=1，b=5

查看试题解析
6. 一元二次方程x²﹣8x＝﹣17的根的情况是（）

A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
7. 下列各组线段的长度成比例的是（）

A、4，6，10，12 B、 $\sqrt{3}$ ， $\sqrt{6}$ ， $\sqrt{7}$ ， $\sqrt{14}$ C、8，15，16，32 D、10，16，12.8，25.6

查看试题解析
8. 用配方法解方程 x²﹣8x+1＝0 时，方程可变形为（）

A、(x﹣4)²＝15 B、(x﹣1)²＝15 C、(x﹣4)²＝1 D、(x+4)²＝15

查看试题解析
9. 如图，利用标杆BE测量建筑物的高度.如果标杆BE高1.2m，测得AB＝1.6m，BC＝12.6m，则楼高CD是（）

A、9.45m B、10.65m C、14.2mm D、16.8m

查看试题解析
10. 已知二次函数y＝x²﹣2x+m²﹣3（m为常数）当﹣1≤x≤2时，函数值y的最小值为﹣3，则m的值为（）

A、1 B、0或﹣1 C、0或1 D、﹣1或1

查看试题解析

二、填空题

11. 若x₁ ， x₂是一元二次方程3x²+7x﹣9＝0的两根，则x₁•x₂的值是.

查看试题解析
12. 如图，△ABC∽△DEF，AM和DN分别是边BC和EF上的高，若S_△ABC：S_△DEF＝1：4，AM＝3，则DN＝.

查看试题解析
13. 方程： $x (x - 2) + x - 2 = 0$ 的解是：.

查看试题解析
14. 如图，二次函数y＝ax²+bx+c的图象与轴交于A、B两点，顶点为C，其中点A、C坐标如图所示，则一元二次方程ax²+bx+c＝0的根是.

查看试题解析
15. 如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝2，GD＝1，DF＝5，那么 $\frac{B C}{C E}$ 的值等于.

查看试题解析
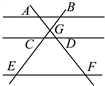16. 如图，二次函数y＝ax²+bx+c的图象是以点C为顶点、经过点B的抛物线，若点B绕点A顺时针旋转90°可得到点C，则a＝.

查看试题解析

三、解答题

17. 解方程：

(1)、x²＋10=7x

(2)、2x²+4x－5=0

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，BC＝3，将△ABC绕点A顺时针旋转90°得到△ADE，连接BD，求BD的长.

查看试题解析
19. 一个二次函数，当自变量x＝0时，函数值y＝﹣1，当x＝﹣2时，y＝0，当x＝2时，y＝6.求这个二次函数的解析式.

查看试题解析
20. 如图，在平面直角坐标系中，△AOC的顶点坐标分别为A（2，2）、O（0，0）、C（ $\frac{5}{2}$ ，0），以原点O为位似中心.

（建议：先用铅笔画图，确定无误后用黑色水性笔画在答题卡上）

(1)、在第一象限内，相似比为 $\frac{1}{2}$ ，将△AOC缩小，不用画图，请直接写出缩小后的△A₁OC₁的两个顶点坐标：A₁ ， C₁

(2)、相似比为2，将△AOC放大在第一象限画出放大后的△A₂OC₂ ，直接写出两个顶点的坐标：A₂ ， C₂；在第三象限画出放大后的△A₃OC₃ ，直接写出两个顶点的坐标：A₃ ， C₃；

(3)、相似比为k，将△AOC放大，若△AOC边上有任意一点P的坐标为（x，y），则放大后的图形上，点P的对应点Q的坐标为.（用含k、x和y的式子表示）.

查看试题解析
21. 某市2016年的人均收入为60000元，2018年的人均收入为72600元.求人均收入的年平均增长率.

查看试题解析
22. 如图，一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA，A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，水流喷出的高度y（m）与水平距离x（m）之间的关系式是 $y = - x^{2} + 2 x + \frac{5}{4}$ （x＞0）

(1)、求水流喷出的最大高度是多少m？此时的水平距离是多少m；

(2)、若不计其他因素，水池的半径OB至少为多少m，才能使喷出的水流不落在池外.

查看试题解析
23. 如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E，AD与BE相交于点F，连接ED.

(1)、求证：△AEF∽△BDF；

(2)、若AE＝4，BD＝8，EF+DF＝9，求DE的长.

查看试题解析
24. 如图，在平面直角坐标系中，直线 $y = \frac{3}{4} x + 3$ 与x轴、y轴分别相交于点A，B，点C在射线OA上，点D在射线OB上，且OD＝2OC，以CD的中点为对称中心作△COD的对称图形△DEC.设点C的坐标为（0，n），△DEC在直线AB下方部分的面积为S.

(1)、当点E在AB上时，n＝，当点D与点B重合时，n＝；

(2)、求S关于n的函数解析式，并直接写出自变量n的取值范围.

查看试题解析
25. 阅读下面材料，完成（1）～（3）题.
数学课上，老师出示了这样一道题：

如图1，△ABC中，AC＝BC＝a，∠ACB＝90°，点D在AB上，且AD＝kAB（其中0＜k＜ $\frac{1}{2}$ ），直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E，探究线段DC、DE的数量关系，并证明.

同学们经过思考后，交流了自己的想法：

小明：“通过观察和度量，发现DC与DE相等”；

小伟：“通过构造全等三角形，经过进一步推理，可以得到DC与DE相等”

小强：“通过进一步的推理计算，可以得到BE与BC的数量关系”

老师：“保留原题条件，连接CE交AB于点O.如果给出BO与DO的数量关系，那么可以求出CO•EO的值”

(1)、在图1中将图补充完整，并证明DC＝DE；

(2)、直接写出线段BE与BC的数量关系（用含k的代数式表示）；

(3)、在图2中将图补充完整，若BO＝ $\frac{5}{13}$ DO，求CO•EO的值（用含a的代数式表示）.

查看试题解析
26. 定义：将函数C的图象绕点P（0，n）旋转180°，得到新的函数C₁的图象，我们称函数C₁是函数C关于点P的相关函数.
例如：当n＝1时，函数 $y = \frac{1}{2} {(x - 6)}^{2} + 3$ 关于点P（0，1）的相关函数为 $y = - \frac{1}{2} {(x + 6)}^{2} - 1$ .

(1)、当n＝0时，
①二次函数y＝x²关于点P的相关函数为；

②点A（2，3）在二次函数y＝ax²﹣2ax+a（a≠0）关于点P的相关函数的图象上，求a的值；

(2)、函数 $y = - x^{2} + \frac{5}{3} \sqrt{2}$ 关于点P的相关函数是 $y = x^{2} - \frac{7 \sqrt{2}}{4}$ ，则n＝；

(3)、当 $\frac{3}{4}$ n﹣1≤x≤ $\frac{3}{4}$ n+3时，函数 $y = - 2 x^{2} + n x - \frac{9}{8} n^{2}$ 的相关函数的最小值为7，求n的值.

查看试题解析