辽宁省鞍山市铁西区、立山区2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列航空公司的标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的方程（a﹣1）x^|a|+1﹣3x+2＝0是一元二次方程，则（）

A、a≠±1 B、a＝1 C、a＝﹣1 D、a＝±1

查看试题解析
3. 若2是一元二次方程x²+mx﹣4m＝0的一个根，则另一个根是（）

A、﹣4 B、4 C、﹣6 D、6

查看试题解析
4. 若 $\frac{2 x - y}{x + y} = \frac{2}{3}$ ，则 $\frac{y}{x}$ 的值为（）

A、 $- \frac{4}{5}$ B、 $\frac{4}{5}$ C、1 D、5

查看试题解析
5. 如图，将△ABC绕点C顺时针旋转90°得到△EDC ．若点A ， D ， E在同一条直线上，∠ACB=20°，则∠ADC的度数是（）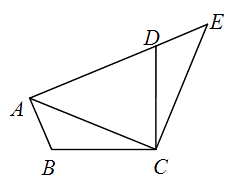

A、55° B、60° C、65° D、70°

查看试题解析
6. 如图，在△ABC中，点D、E分别在边AB，AC上，连接CD、BE交于点O，且DE∥BC，OD＝1，OC＝3，AD＝2，则AB的长为（　　）

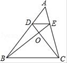A、4 B、6 C、8 D、9

查看试题解析
7. 用配方法解下列方程时，配方有错误的是（）

A、 $x^{2} - 2 x - 99 = 0$ 化为 ${(x - 1)}^{2} = 100$ B、 $2 x^{2} - 7 x - 4 = 0$ 化为 ${(x - \frac{7}{4})}^{2} = \frac{81}{16}$ C、 $x^{2} + 8 x + 9 = 0$ 化为 ${(x + 4)}^{2} = 25$ D、 $3 x^{2} - 4 x - 2 = 0$ 化为 ${(x - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
8. 已知 $a ， b$ 是非零实数， $| a | > | b |$ ，在同一平面直角坐标系中，二次函数 $y_{1} = a x^{2} + b x$ 与一次函数 $y_{2} = a x + b$ 的大致图象不可能是（）

A、 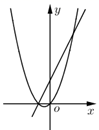B、 C、 D、

查看试题解析

二、填空题

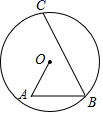
9. 一元二次方程x²﹣2x﹣5＝0和x²+4x+5＝0的所有实数根的和等于.

查看试题解析
10. 已知二次函数的图象经过点 $P (2 ， 2)$ ，顶点为 $O (0 ， 0)$ 将该图象向右平移，当它再次经过点 $P$ 时，所得抛物线的函数表达式为.

查看试题解析
11. 如图，⊙O内有一条弦BC，A为⊙O内一点、其中OA＝3，AB＝4，∠A＝∠B＝60°，则弦BC的长为.

查看试题解析
12. 在平面直角坐标系中，点 $A, B$ 的坐标分别是 $A (4, 2), B (5, 0)$ ，以点 $O$ 为位似中心，相们比为 $\frac{1}{2}$ ，把 $△ A B O$ 缩小，得到 $△ A_{1} B_{1} O$ ，则点 $A$ 的对应点 $A_{1}$ 的坐标为.

查看试题解析
13. 若二次函数y＝4x²﹣6x﹣3的图象与x轴交于点A（x₁ ， 0），B（x₁ ， 0）两点，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为.

查看试题解析
14. 股市规定：股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再涨，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停．若一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为x，则x满足的方程是．

查看试题解析
15. 如图，菱形OABC的顶点O在坐标原点，顶点A在x轴上，∠B＝120°，OA＝1，将菱形OABC绕原点顺时针旋转105°至OA'B′C'的位置，则点B'的坐标为.

查看试题解析
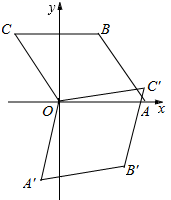16.
在如图所示的平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₂A₂B₁与△OA₁B₁关于点B₁成中心对称，再作△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，如此作下去，则△B_2nA_2n+1B_2n+1（n是正整数）的顶点A_2n+1的坐标是．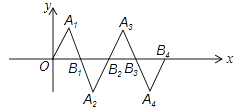

查看试题解析

三、解答题

17.

(1)、解方程： ${(2 x - 1)}^{2} = x (3 x + 2) - 7$

(2)、用配方法解方程： $2 x^{2} - 3 x + \frac{1}{2} = 0$

查看试题解析
18. 如图，图中的小方格都是边长为1的正方形，△ABC的A，B，C三点坐标为A（2，0）、B（2，2）、C（6，3）。

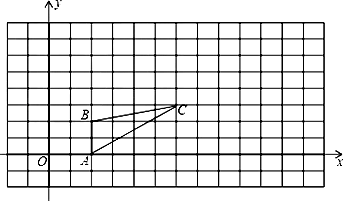(1)、请在图中画出一个△ $A^{'} B^{'} C^{'}$ ，使△ $A^{'} B^{'} C^{'}$ 与△ABC是以坐标原点为位似中心，相似比为2的位似图形。

(2)、求△ $A^{'} B^{'} C^{'}$ 的面积。

查看试题解析
19. 关于的一元二次方程x²+2x+k+1=0的实数解是x₁和x₂ ．

(1)、求k的取值范围；

(2)、如果x₁+x₂﹣x₁x₂＜﹣1且k为整数，求k的值．

查看试题解析
20. 如图，在甲、乙两座楼正中间有一堵院墙，小明站在甲楼某层窗口前，同时小光站在乙楼某层窗口前观察这堵墙，小明视线所及位置如图所示，小光视线恰好落在甲楼底部.已知墙的高度为5米，两栋楼的间距为100米，小明视线所及位置到墙的距离为10米.

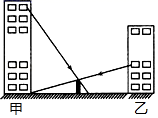(1)、请根据题意画出平面图形，并标上相应字母.

(2)、求甲、乙两人的观测点到地面高度的距离差.

查看试题解析
21. 如图，一圆弧形桥拱的圆心为 $E$ ，拱桥的水面跨度 $A B = 80$ 米，桥拱到水面的最大高度 $D F$ 为 $20$ 米.求：

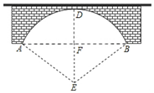(1)、桥拱的半径；

(2)、现水面上涨后水面跨度为 $60$ 米，求水面上涨的高度为米.

查看试题解析
22. 在矩形ABCD中，已知AD＞AB.在边AD上取点E，使AE＝AB，连结CE，过点E作EF⊥CE，与边AB或其延长线交于点F.

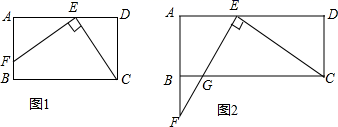(1)、如图1，当点F在边AB上时，线段AF与DE的大小关系为.

(2)、如图2，当点F在边AB的延长线上时，EF与边BC交于点G.判断线段AF与DE的大小关系，并加以证明.

(3)、如图2，若AB＝2，AD＝5，求线段BG的长.

查看试题解析
23. 随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点.抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆.已知2006年底全市汽车拥有量为10万辆.

(1)、求2006年底至2008年底我市汽车拥有量的年平均增长率；

(2)、为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）

查看试题解析
24. 某店铺经营某种品牌童装，购进时的单价是40元，根据市场调查，当销售单价是60元时，每天销售量是200件，销售单价每降低1元，就可多售出20件.

(1)、求出销售量y件）与销售单价x（元）之间的函数关系式；

(2)、求出销售该品牌童装获得的利润W（元）与销售单价x元）之间的函数关系式；

(3)、若装厂规定该品牌童装的销售单价不低于56元且不高于60元，则此服装店销售该品牌童装获得的最大利润是多少？

查看试题解析
25. 如图1是实验室中的一种摆动装置， $B C$ 在地面上，支架 $A B C$ 是底边为 $B C$ 的等腰直角三角形，摆动臂长 $A D$ 可绕点A旋转，摆动臂 $D M$ 可绕点D旋转， $A D = 30$ ， $D M = 10$ .

(1)、在旋转过程中：
①当 $A ， D ， M$ 三点在同一直线上时，求 $A M$ 的长；

②当 $A ， D ， M$ 三点在同一直角三角形的顶点时，求 $A M$ 的长.

(2)、若摆动臂 $A D$ 顺时针旋转 $90 °$ ，点 $D$ 的位置由 $△ A B C$ 外的点 $D_{1}$ 转到其内的点 $D_{2}$ 处，连结 $D_{1} D_{2}$ ，如图2，此时 $∠ A D_{2} C = 135 °$ ， $C D_{2} = 60$ ，求 $B D_{2}$ 的长.

查看试题解析
26. 如图，已知抛物线与坐标轴交于A（﹣4，0）、B（2，0）、C（0，4），连接BC，AC.

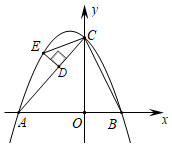(1)、求抛物线的解析式；

(2)、若点E是抛物线在第二象限上的一点，过点E作DE⊥AC于点D，求DE的最大值.

(3)、若点E是抛物线上第二象限上的一动点，过点E作DE⊥AC于点D，连接CE，若△CDE与△COB相似，直接写出点E的坐标.

查看试题解析