辽宁省鞍山市台安县2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 下列方程中,属于一元二次方程的是( )A、 B、 C、 D、2. 下列图形中,一定既是轴对称图形又是中心对称图形的是( ).A、等边三角形 B、直角三角形 C、平行四边形 D、正方形3. 在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A、y=3(x+1)2+2 B、y=3(x+1)2﹣2 C、y=3(x﹣1)2+2 D、y=3(x﹣1)2﹣24. 下列说法中,不正确的个数是( )①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.
A、1个 B、2个 C、3个 D、4个5. 若三角形两边长分别为3和4,第三边的长是方程 的根,则此三角形的周长为( )A、12 B、14 C、12或14 D、13或156. 如图,在 中, ,将 绕着点 按逆时针方向旋转到 的位置,使点 落在 延长线上的点 处,则 为( ) A、95° B、85° C、90° D、80°7. 如图⊙O的直径 垂直于弦 ,垂足是 , , , 的长为( )
A、95° B、85° C、90° D、80°7. 如图⊙O的直径 垂直于弦 ,垂足是 , , , 的长为( ) A、
A、 B、4
C、
B、4
C、 D、8
8. 如图,等边 边长为2,四边形 是平行四边形, , 和 在同一条直线上,且点 与点 重合,现将 沿 的方向以每秒1个单位的速度匀速运动,当点 与点 重合时停止,则在这个运动过程中, 与四边形 的重合部分的面积 与运动时间 之间的函数关系图象大致是( )
D、8
8. 如图,等边 边长为2,四边形 是平行四边形, , 和 在同一条直线上,且点 与点 重合,现将 沿 的方向以每秒1个单位的速度匀速运动,当点 与点 重合时停止,则在这个运动过程中, 与四边形 的重合部分的面积 与运动时间 之间的函数关系图象大致是( ) A、
A、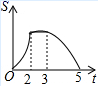 B、
B、 C、
C、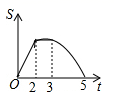 D、
D、
二、填空题
-
9. 写出一个开口向上,且顶点为 的抛物线解析式为。10. 在平面直角坐标系中,点A(-2,1)关于原点对称的点的坐标是.11. 设 是方程 的两个实数根,则 的值是.12. 如图,已知 为四边形 的外接圆,若 ∠BCD=120°,则 度数为。
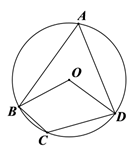 13. 如图,在边长为12的正方形 中,点 在边 上, ,把线段 绕点 旋转使点 落在线段 上的点 处,则 两点之间的距离为。
13. 如图,在边长为12的正方形 中,点 在边 上, ,把线段 绕点 旋转使点 落在线段 上的点 处,则 两点之间的距离为。 14. 如图, 分别与 相切于点 , 的切线 分别交 于点 ,切点 在 上,若 的周长为 ,则 的长是 。
14. 如图, 分别与 相切于点 , 的切线 分别交 于点 ,切点 在 上,若 的周长为 ,则 的长是 。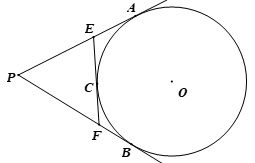 15. 抛物线 的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是直线 。给出下列结论:① ;② ;③方程 有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为 ,其中正确的结论有。其中正确的有。(只需填写序号即可)
15. 抛物线 的部分图象如图所示,与 轴的一个交点坐标为 ,抛物线的对称轴是直线 。给出下列结论:① ;② ;③方程 有两个不相等的实数根;④抛物线与x轴的另一个交点坐标为 ,其中正确的结论有。其中正确的有。(只需填写序号即可)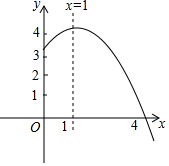 16. 在平面直角坐标系中,直线l: 与x轴交于点 ,如图所示依次作正方形 、正方形 、…、正方形 ,使得点 …在直线l上,点 …在y轴正半轴上,则点 的横坐标是。
16. 在平面直角坐标系中,直线l: 与x轴交于点 ,如图所示依次作正方形 、正方形 、…、正方形 ,使得点 …在直线l上,点 …在y轴正半轴上,则点 的横坐标是。
三、解答题
-
17. 用适当方法解方程:18. 如图,在平面直角坐标系中,已知 的三个顶点坐标分别是 .

( 1 )将 向下平移5个单位后得到 ,请画出 ;
( 2 )将 绕原点 逆时针旋转90°后得到 ,请画出 ;
19. 已知关于 的方程 。(1)、若该方程的一个根是 ,求 的值及该方程的另一个根;(2)、求证:不论 取何实数,该方程都有两个不相等的实数根。20. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度,2011年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2013年底三年共累计投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(1)、求每年市政府投资的增长率;(2)、若这两年内的建设成本不变,求到2013年底共建设了多少万平方米廉租房.21. 如图, 为 的直径, 于点 , 是弧AC上的动点,连接 分别交 , 于点 , .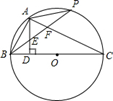 (1)、当 时, 与 相等吗?为什么?(2)、当点 在什么位置时, ?证明你的结论.22. 如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)、当 时, 与 相等吗?为什么?(2)、当点 在什么位置时, ?证明你的结论.22. 如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点. (1)、求抛物线解析式.(2)、将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.23. 如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF.
(1)、求抛物线解析式.(2)、将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.23. 如图,AB是⊙O的直径,点C,D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA的延长线与OC的延长线于点E,F,连接BF. (1)、求证:BF是⊙O的切线;(2)、已知圆的半径为1,求EF的长.24. 在汛期到来之际,某水泵厂接到生产一批小型抽水泵的紧急任务。要求必须在10天内(含10天)完成任务。为提高生产效率,工厂加班加点,接到任务的第一天就生产了水泵20台,以后每天生产的水泵都比前一天多2 台。由于机器损耗等原因,当日生产的水泵数量达到28台后,每多生产一台,当天生产的所有水泵,平均每台成本就增加20元。(1)、设第 天生产水泵 台,直接写出 与 之间的函数解析式,并写出自变量 的取值范围;(2)、若每台水泵的成本价(日生产量不超过28台时)为1000元,销售价格为每台1400元,设第 天的利润为 元,试求 与 之间的函数解析式,并求该厂哪一天获得的利润最大,最大利润最多少?25. 在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.(1)、如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;
(1)、求证:BF是⊙O的切线;(2)、已知圆的半径为1,求EF的长.24. 在汛期到来之际,某水泵厂接到生产一批小型抽水泵的紧急任务。要求必须在10天内(含10天)完成任务。为提高生产效率,工厂加班加点,接到任务的第一天就生产了水泵20台,以后每天生产的水泵都比前一天多2 台。由于机器损耗等原因,当日生产的水泵数量达到28台后,每多生产一台,当天生产的所有水泵,平均每台成本就增加20元。(1)、设第 天生产水泵 台,直接写出 与 之间的函数解析式,并写出自变量 的取值范围;(2)、若每台水泵的成本价(日生产量不超过28台时)为1000元,销售价格为每台1400元,设第 天的利润为 元,试求 与 之间的函数解析式,并求该厂哪一天获得的利润最大,最大利润最多少?25. 在△ABC中,AC=BC,∠ACB=90°,点D为AC的中点.(1)、如图1,E为线段DC上任意一点,将线段DE绕点D逆时针旋转90°得到线段DF,连接CF,过点F作FH⊥FC,交直线AB于点H.判断FH与FC的数量关系并加以证明;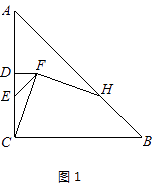 (2)、如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.
(2)、如图2,若E为线段DC的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明.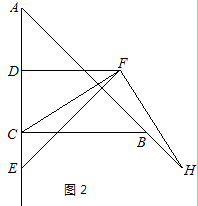 26. 如图,已知抛物线 与x轴交于点 和点 ,与 轴交于点 .
26. 如图,已知抛物线 与x轴交于点 和点 ,与 轴交于点 .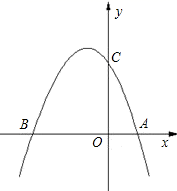 (1)、求抛物线的解析式;(2)、若点 为第二象限抛物线上一动点,连接 ,求 面积的最大值,并求此时 点的坐标.(3)、在抛物线上是否存在点 使得 为等腰三角形?若存在,请求出一共有几个符合条件的点 (简要说明理由)并写出其中一个点的坐标;若不存在这样的点 ,请简要说明理由.
(1)、求抛物线的解析式;(2)、若点 为第二象限抛物线上一动点,连接 ,求 面积的最大值,并求此时 点的坐标.(3)、在抛物线上是否存在点 使得 为等腰三角形?若存在,请求出一共有几个符合条件的点 (简要说明理由)并写出其中一个点的坐标;若不存在这样的点 ,请简要说明理由.