湖北省孝感市云梦县2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 若关于x的方程（m﹣2）x2+mx﹣1=0是一元二次方程，则m的取值范围是（   ）
    A、m≠2 B、m=2 C、m≥2 D、m≠0

    查看试题解析

  • 2. 抛物线y=﹣2（x+1）2﹣3的顶点坐标是（   ）
    A、（1，3） B、（﹣1，﹣3） C、（1，﹣3） D、（﹣1，3）

    查看试题解析

  • 3. 用配方法解方程 x2﹣6x﹣5＝0，下列配方结果正确的是（     ）
    A、（x﹣6）2＝41 B、（x﹣3）2＝14 C、（x+3）2＝14 D、（x﹣3）2＝4

    查看试题解析

  • 4. 把抛物线y=3x2先向上平移2个单位，再向右平移3个单位，所得的抛物线是（   ）
    A、y=3（x+3）2﹣2 B、y=3（x+3）2+2 C、y=3（x﹣3）2﹣2 D、y=3（x﹣3）2+2

    查看试题解析

  • 5. 如图，△ABC的顶点都在⊙O上，∠BAO＝50°，则∠C的度数为（   ）

    A、30° B、40° C、45° D、50°

    查看试题解析

  • 6. 如图，在Rt△ABC中，∠BAC＝90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C，点A在边B′C上，则∠B′的大小为（ ）

    A、42° B、48° C、52° D、58°

    查看试题解析

  • 7. 某品牌手机经过连续两次降价，每台售价由原来的3456元降到了2400元，设平均每次降价的百分率为x，则可列方程（   ）
    A、3456（1+x）2＝2400 B、2400（1+x）2 ＝3456 C、3456（1﹣x）2 ＝2400 D、2400（1-x）2＝3456

    查看试题解析

  • 8. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1 ， 则其旋转中心可能是（   ）

    A、点A B、点B C、点C D、点D

    查看试题解析

  • 9. 如图1，在△ABC中，AB＝AC，BC＝m，D，E分别是AB，AC边的中点，点P为BC边上的一个动点，连接PD，PA，PE.设PC＝x，图1中某条线段长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线可能是（   ）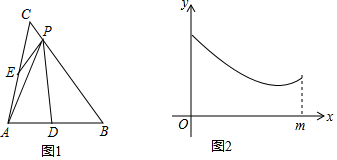

    A、PB B、PE C、PA D、PD

    查看试题解析

  • 10. 抛物线y＝ax2+bx+1的顶点为D，与x轴正半轴交于A，B两点，A在B左，与y轴正半轴交于点C，当△ABD和△OBC均为等腰直角三角形（O为坐标原点）时，b的值为（   ）

    A、2 B、﹣2或﹣4 C、﹣2 D、﹣4

    查看试题解析

二、填空题

  • 11. 点 P(−3,4) 关于原点的对称点的坐标为.

    查看试题解析

  • 12. 已知二次函数y＝ax2+3ax+c的图象与x轴的一个交点为（﹣4，0），则它与x轴的另一个交点的坐标是.

    查看试题解析

  • 13. 若关于x的一元二次方程（m﹣1）x2+x+m2﹣1＝0有一个根为0，则m的值为.

    查看试题解析

  • 14. 某种植物的主干长出若干数目的支干又长出同样数目的小分支，主干、支干和小分支的总数是91．设每个支干长出x个小分支，则可得方程为 ．

    查看试题解析

  • 15. 如图，在⊙O中，AB是直径，弦BE的垂直平分线交⊙O于点C，CD⊥AB于D，AD＝1，BE＝6，则BD的长为.

    查看试题解析

  • 16. 已知二次函数y＝x2﹣2x+2在t≤x≤t+1时的最小值是t，则t的值为.

    查看试题解析

三、解答题

  • 17. 解方程：
    (1)、x2﹣4x﹣1＝0
    (2)、3x2﹣5x+1＝0

    查看试题解析

  • 18. 如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（1，1），B（4，2），C（3，5）.

    (1)、求△ABC的面积；
    (2)、在图中画出△ABC绕点A逆时针旋转90°得到的△A'B'C'，并写出点C的对应点C'的坐标.

    查看试题解析

  • 19. 如图是一张长12dm，宽6dm的长方形纸板，将纸板四个角各剪去一个同样的边长为xdm的正方形，然后将四周突出部分折起，可制成一个无盖长方体纸盒.

    (1)、无盖方盒盒底的长为dm，宽为dm（用含x的式子表示）.
    (2)、若要制作一个底面积是40dm2的一个无盖长方体纸盒，求剪去的正方形边长x.

    查看试题解析

  • 20. 已知关于x的一元二次方程x2+（2k+1）x+k2﹣1＝0.
    (1)、若该方程有两个不相等的实数根，求k的最小整数值；
    (2)、若方程的两个实数根为x1 ， x2 ， 且（x1﹣x2）2+k2＝17，求k的值.

    查看试题解析

  • 21. 某商品现在的售价为每件25元，每天可售出50件，市场调查发现，售价每上涨1元，每天就少卖出2件，已知该商品的进价为每件20元，设该商品每天的销售量为y件，售价为每件x元（x为正整数）
    (1)、求y与x之间的函数关系式；
    (2)、该商品的售价定为每件多少元时，每天的销售利润W（元）最大，最大利润是多少元？

    查看试题解析

  • 22. 已知⊙O的半径为5，点A、B、C都在⊙O上，∠CAB的平分线交⊙O于点D.

    (1)、如图1，若BC为⊙O的直径，AB＝6，求AC和BD的长；
    (2)、如图2，若∠CAB＝60°，过圆心O作OE⊥BD于点E，求OE的长.

    查看试题解析

  • 23. 在正方形ABCD和正方形AEFG中，点B在边AG上，点D在线段EA的延长线上，连接BE.

    (1)、如图1，求证：DG⊥BE；
    (2)、如图2，将正方形ABCD绕点A按逆时针方向旋转，使点B恰好落在线段DG上.

    ①求证：DG⊥BE；

    ②若AB＝2，AG＝3，求线段BE的长.

    查看试题解析

  • 24. 已知：如图，抛物线y＝ax2+bx﹣3与x轴交于A点，与y轴交于C点，且A（1，0）、B（3，0），点D是抛物线的顶点.

    (1)、求抛物线的解析式
    (2)、在y轴上是否存在M点，使得△MAC是以AC为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由.
    (3)、点P为抛物线上的动点，且在对称轴右侧，若△ADP面积为3，求点P的坐标.

    查看试题解析