湖北省武汉市江夏区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 一元二次方程 的二次项系数、一次项系数分别是A、3, B、3,1 C、 ,1 D、3,62. 下列图形绕某点旋转180°后,不能与原来图形重合的是( )A、
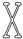 B、
B、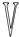 C、
C、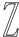 D、
D、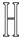 3. 与抛物线 的形状、开口方向都相同,只有位置不同的抛物线是( )A、 B、 C、 D、4. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣35. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )
3. 与抛物线 的形状、开口方向都相同,只有位置不同的抛物线是( )A、 B、 C、 D、4. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣35. 如图,⊙O是△ABC的外接圆,∠ACO=45°,则∠B的度数为( )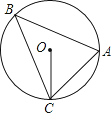 A、30° B、35° C、40° D、45°6. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B =78°,则∠CC'B'的大小是( )
A、30° B、35° C、40° D、45°6. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠B =78°,则∠CC'B'的大小是( )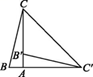 A、23° B、30° C、33° D、39°7. 若A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=2(x-1)2+3上的三个点,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y28. 已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
A、23° B、30° C、33° D、39°7. 若A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=2(x-1)2+3上的三个点,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y28. 已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:X
…
﹣1
0
1
2
3
…
y
…
5
1
﹣1
﹣1
1
…
则该函数的对称轴为( )
A、y轴 B、直线x= C、直线x=2 D、直线x=9. 已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0,
则正确的结论是( )
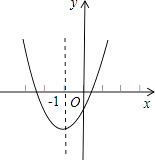 A、①②③④ B、②④⑤ C、②③④ D、①④⑤10. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
A、①②③④ B、②④⑤ C、②③④ D、①④⑤10. 如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )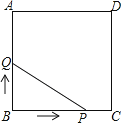 A、
A、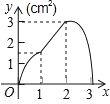 B、
B、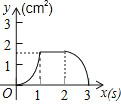 C、
C、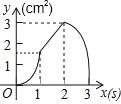 D、
D、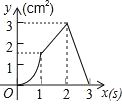
二、填空题
-
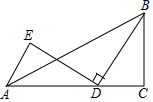
11. 点(-2,5)关于原点对称的点的坐标是 .12. 抛物线y=x2-2x-2的顶点坐标是.13. 某村种的水稻前年平均每公顷产7200千克,今年平均每公顷产8450千克,设这两年该村每公顷产量的年平均增长率为x,根据题意,所列方程为.14. 汽车刹车后行驶的距离s与行驶时间t(秒)的函数关系是s=15t﹣6t2 , 汽车从刹车到停下来所用时间是秒.15. 抛物线y=ax2+2ax+c经过点A(﹣3,0),则关于x的一元二次方程ax2+2ax+c=0的解是.16. 如图,在△ABC中,∠C=90°,BC=3,AC=5,点D为线段AC上一动点,将线段BD绕点D逆时针旋转90°,点B的对应点为E,连接AE,则AE长的最小值为.
三、解答题
-
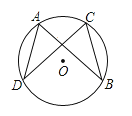
17. 解方程:x2﹣4x﹣3=0.18. 如图,在⊙O中,AD=BC,求证:DC=AB.
 19. 已知一元二次方程 有两个根分别为 .(1)、求 的取值范围;(2)、若原方程的两个根 满足 ,求 的值.20. 如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
19. 已知一元二次方程 有两个根分别为 .(1)、求 的取值范围;(2)、若原方程的两个根 满足 ,求 的值.20. 如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.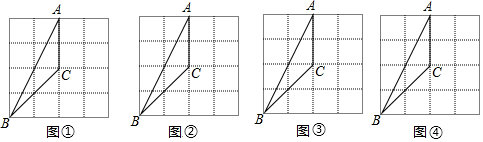
( 1 )在图1中,画出一个与△ABC成中心对称的格点三角形;
( 2 )在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
( 3 )在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形;
( 4 )在图4中,画出所有格点△BCD,使△BCD为等腰直角三角形,且S△BCD=4.
21. 已知A,B,C,D是⊙O上的四个点.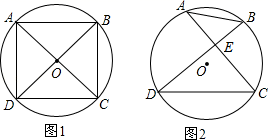 (1)、如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)、如图2,若AC⊥BD.垂足为E,AB=4,DC=6,求⊙O的半径.22. 某服装公司的某种运动服每月的销量与售价的关系信息如表:
(1)、如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;(2)、如图2,若AC⊥BD.垂足为E,AB=4,DC=6,求⊙O的半径.22. 某服装公司的某种运动服每月的销量与售价的关系信息如表:售价x(元/件)
100
110
120
130
…
月销量y(件)
200
180
160
140
…
已知该运动服的进价为每件60元,设售价为x元.
(1)、请用含x的式子表示:①销量该运动服每件的利润是元;
②月销量是y=;(直接写出结果)
(2)、设销售该运动服的月利润为w元,那么售价为多少时,当月的利润最大,最大利润时多少?(3)、该公司决定每销售一件运动服,就捐赠a(a>0)元利润给希望工程,物价部门规定该运动服售价不得超过120元,设销售该运动服的月利润为w元,若月销售最大利润是8800元,求a的值.23. 如图1,若四边形ABCD、GFED都是正方形,显然图中有AG=CE,AG⊥CE.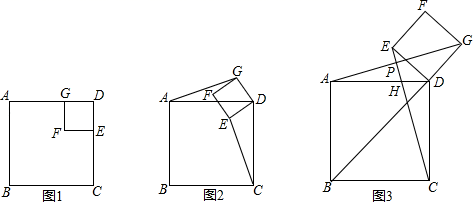 (1)、当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明,若不成立,请说明理由;(2)、当正方形GFED绕D旋转到B,D,G在一条直线(如图3)上时,连结CE,设CE分别交AG、AD于P、H.
(1)、当正方形GFED绕D旋转到如图2的位置时,AG=CE是否成立?若成立,请给出证明,若不成立,请说明理由;(2)、当正方形GFED绕D旋转到B,D,G在一条直线(如图3)上时,连结CE,设CE分别交AG、AD于P、H.①求证:AG⊥CE;
②如果,AD=2 ,DG= ,求CE的长.
24. 已知抛物线的顶点H(2,0),经过点A(1,1),与y轴交于点C.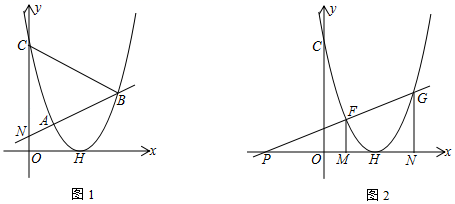 (1)、求抛物线的解析式;(2)、如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;(3)、如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PM•PN的值.
(1)、求抛物线的解析式;(2)、如图1,在线段OC(端点除外)上是否存在一点N,直线NA交抛物线于另一点B,满足BC=BN?若存在,请求出点N的坐标;若不存在,请说明理由;(3)、如图2,过点P(﹣3,0)作直线交抛物线于点F、G,FM⊥x轴于M,GN⊥x轴于N,求PM•PN的值.