湖北省随州市高新区2020届九年级上学期数学期中考试试卷
试卷更新日期：2020-10-09 类型：期中考试
一、选择题
-
1. 下列图形中既是中心对称图形又是轴对称图形的是A、
B、
C、
D、
2. 二次函数y＝﹣x2+2x+4的顶点坐标是（ ）A、（﹣1，5） B、（1，5） C、（﹣1，﹣5） D、（1，﹣5）3. 已知互不相等的实数m、n，且满足m2+3m﹣5＝0，n2+3n﹣5＝0，则m2﹣n2+mn+6m的值为（ ）A、14 B、﹣14 C、10 D、﹣104. 如图，四边形ABCD内接于⊙O，已知∠BCE=70°，则∠A的度数是（ ）
A、110° B、70° C、55° D、35°5. 已知圆的直径为10cm，如果圆心与直线的距离是6cm，那么直线和圆的公共点的个数为（ ）A、0 B、1 C、2 D、36. 下列说法中，正确的个数为：①在等圆中，等弦对等弧；②直径是圆的对称轴；③平分弦的直径垂直于这条弦；④弦的中垂线一定经过圆心.（ ）A、0 B、1 C、2 D、37. 以坐标原点为旋转中心，把点A（3，6）逆时针旋转90°，得到点B，则点B关于y轴对称的点的坐标为（ ）A、（6，3） B、（﹣3，﹣6） C、（6，﹣3） D、（﹣6，3）8. 已知（x2+y2）（x2+y2﹣4）＝5，则x2+y2的值为（ ）A、1 B、﹣1或5 C、5 D、1或﹣59. 若二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的是（ ）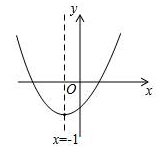
A、a＞b＞c B、b＞a＞c C、c＞a＞b D、c＞b＞a10. 已知两点M（6，y1），N（2，y2）均在抛物线y＝ax2+bx+c（a≠0）上，点P（x0 ， y0）是抛物线的顶点，若y0≤y2＜y1 ， 则x0的取值范围是（ ）A、x0＜4 B、x0＞﹣2 C、﹣6＜x0＜﹣2 D、﹣2＜x0＜2二、填空题
-
11. 已知点 P（m，1）与点 P′（5，n）关于点 A（﹣2，3）对称，则 m﹣n＝.12. 如图，PA、PB分别与⊙O相切于A、B两点，若∠P=52°，则∠C的度数为.
13. 已知⊙O的直径为10，圆心O（4，5），则⊙O截y轴所得的弦长为.14. 某公司今年元月份利润为500万元，以后两个月均匀增长，第一季度的利润1820万元，设该公司利润月平均增长率为x，根据题意可列方程.15. 已知关于x的函数y＝（m﹣1）x2+（2m﹣1）x+m+2的图象与x轴只有一个交点，则m＝.16. （定义[a，b，c]为函数 的特征数，下面给出特征数为 [2m，1－m，－1－m]的函数的一些结论：①当m＝－3时，函数图象的顶点坐标是（ ， ）；
②当m>0时，函数图象截x轴所得的线段长度大于 ；
③当m<0时，函数在 时，y随x的增大而减小；
④当m≠0时，函数图象经过x轴上一个定点.
其中正确的结论有.（只需填写序号）
三、解答题
-
17. 直角坐标系第二象限内的点P（x2+2x，3）与另一点Q（x+2，y）关于原点对称，试求x+2y的值．18. 已知关于x的一元二次方程x2﹣3x+m﹣2＝0有两个实数根x1 ， x2.(1)、求m的取值范围；(2)、若x1 ， x2满足2x1＝|x2|+1，求m的值.19. 某超市销售一种成本为每千克40元的水产品，经市场分析，若按每千克50元销售，一个月能销售出500千克；销售单价每涨价1元，月销售量就减少10千克。针对这种水产品的销售情况，要使得月销售利润达到8000元，又要“薄利多销”，销售单价应定为多少？20. 已知，如图，平行四边形ABCD中，AB⊥AC，AB=1，BC= ，对角线AC，BD交于O点，将直线AC绕点O顺时针旋转，分别交BC，AD于点E，F.
(1)、求证：当旋转角为90°时，四边形ABEF是平行四边形；(2)、在旋转过程中，四边形BEDF可能是菱形吗？如果不能，请说明理由；如能，说明理由并求出此时AC绕点O顺时针旋转的度数.21. 如图，在平面直角坐标系xOy中，点A（6，0），B（0，6 ），点P为线段AB上的动点，PC⊥OA于C，PD⊥OB于D，当矩形PCOD的邻边之比为1：2时，求点P的坐标.
22. 如图，已知△ABC是等边三角形，以AB为直径作⊙O，交BC边于点D，交AC边于点F，作DE⊥AC于点E．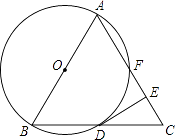
(1)、求证：DE是⊙O的切线；(2)、若△ABC的边长为4，求EF的长度．23. 阅读理解题：学习了二次根式后，你会发现一些含有根号的式子可以写成另一个式子的平方，如3+2 ＝（1+ ）2 ， 我们来进行以下的探索：设a+b ＝（m+n ）2（其中a，b，m，n都是正整数），则有a+b ＝m2+2n2+2mn ，∴a＝m2+2n2 ， b＝2mn，这样就得出了把类似a+b 的式子化为平方式的方法，请仿照上述方法探索并解决下列问题：
(1)、当a，b，m，n都为正整数时，若a+b ＝（m+n ）2 ， 用含m，n的式子分别表示a，b，得a＝ ， b＝.(2)、若a﹣4 ＝（m﹣n ）2且a，m，n都为正整数，求a的值.24. 如图所示，在平面直角坐标系xOy中，有AB为斜边的等腰直角三角形ABC，其中点A（0，2），点C（﹣1，0），抛物线y＝ax2+ax﹣2经过B点.
(1)、求B点的坐标；(2)、求抛物线的解析式；(3)、在抛物线上是否存在点N（点B除外），使得△ACN仍然是以AC为直角边的等腰直角三角形？若存在，求点N的坐标；若不存在，请说明理由.