湖北省鄂州市梁子湖区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 下列是一元二次方程的是A、 B、 C、 D、2. 下列函数关系中,是二次函数的是( )A、在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系 B、当距离一定时,火车行驶的时间t与速度v之间的关系 C、等边三角形的周长C与边长a之间的关系 D、圆的面积S与半径R之间的关系3. 下列四个图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 在平面直角坐标系中,对于抛物线 ,下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线x=2 C、当x<2时,y的值随x值的增大而增大,当x>2时,y的值随x值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到6. 如图,将 绕点C顺时针旋转得到 ,使点A的对应点D恰好落在边 上,点B的对应点为E,连接 .下列结论一定正确的是( )
4. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根5. 在平面直角坐标系中,对于抛物线 ,下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线x=2 C、当x<2时,y的值随x值的增大而增大,当x>2时,y的值随x值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到6. 如图,将 绕点C顺时针旋转得到 ,使点A的对应点D恰好落在边 上,点B的对应点为E,连接 .下列结论一定正确的是( )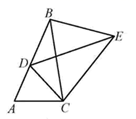 A、 B、 C、 D、7. 某新建火车站站前广场绿化工程中有一块长为20米,宽为12米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为112米2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是( )
A、 B、 C、 D、7. 某新建火车站站前广场绿化工程中有一块长为20米,宽为12米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为112米2 , 两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是( )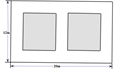 A、2米 B、 米 C、2米或 米 D、3米8. 已知在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,则直线AB关于原点对称的直线的解析式是( )A、 B、 C、 D、9. 在平面直角坐标系中,二次函数 的图象如图所示,下列结论:① ;② ;③ ;④a-b+c<0.其中正确结论的个数是( )
A、2米 B、 米 C、2米或 米 D、3米8. 已知在平面直角坐标系中,直线 与x轴交于点A,与y轴交于点B,则直线AB关于原点对称的直线的解析式是( )A、 B、 C、 D、9. 在平面直角坐标系中,二次函数 的图象如图所示,下列结论:① ;② ;③ ;④a-b+c<0.其中正确结论的个数是( )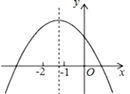 A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系中,抛物线 如图所示.已知点A的坐标为(1,-1),过点A作 轴交抛物线于点 ,过点 作 交抛物线于点 ,过点 作 轴交抛物线于点 ,过点 作 交抛物线于点 ,……,依次进行下去,则点 的坐标为( )
A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系中,抛物线 如图所示.已知点A的坐标为(1,-1),过点A作 轴交抛物线于点 ,过点 作 交抛物线于点 ,过点 作 轴交抛物线于点 ,过点 作 交抛物线于点 ,……,依次进行下去,则点 的坐标为( )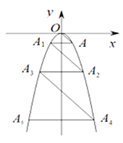 A、(1010,-10102) B、(-1010,-10102) C、(1009,-10092) D、(-1009,-10092)
A、(1010,-10102) B、(-1010,-10102) C、(1009,-10092) D、(-1009,-10092)二、填空题
-
11. 一元二次方程 的一个根是 ,则m的值是.12. 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是 ,则小球从抛出到落地所用的时间是 s.13. 如图,在平面直角坐标系xOy中,直线y= x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
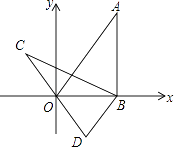 14. 阅读材料:如果a,b分别是一元二次方程 的两个实数根,则有 , ;创新应用:如果m,n是两个不相等的实数,且满足 , ,那么代数式 的值是 .15. 已知二次函数 及一次函数 ,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线 与新图象有3个交点时,m的值是.
14. 阅读材料:如果a,b分别是一元二次方程 的两个实数根,则有 , ;创新应用:如果m,n是两个不相等的实数,且满足 , ,那么代数式 的值是 .15. 已知二次函数 及一次函数 ,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线 与新图象有3个交点时,m的值是.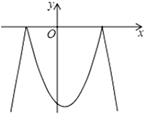 16. 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
16. 如图,线段AB=10,点P在线段AB上,在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF,点M、N分别是EF、CD的中点,则MN的最小值是 .
三、解答题
-
17. 解方程:(1)、 ;(2)、 .18. 已知:在平面直角坐标系中, 的三个顶点的坐标分别为 , , .
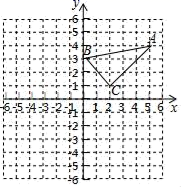
( 1 )画出 关于原点成中心对称的 ,并写出点 的坐标;
( 2 )画出将 绕点 按顺时针旋转 所得的 .
19. 5G时代即将来临,湖北省提出“建成全国领先、中部一流5G网络”的战略目标.据统计,目前湖北5G基站的数量有1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.(1)、按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率;(2)、若2023年保持前两年5G基站数量的年平均增长率不变,到2023年底,全省5G基站数量能否超过29万座?20. 已知关于x的一元二次方程 有两个不相等的实数根 , .(1)、若a为正整数,求a的值;(2)、若 , 满足 ,求a的值.21. 如图,在平面直角坐标系中,二次函数 的图象交x轴于点A,B(点A在点B的左侧).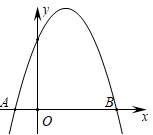 (1)、求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;(2)、把点B向上平移m个单位得点B1 . 若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m , n的值.22. 如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)、求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;(2)、把点B向上平移m个单位得点B1 . 若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m , n的值.22. 如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G. (1)、如图1,当点 E 落在 CD 边上时,求线段 CE 的长;(2)、如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;(3)、在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.23. 某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元/件( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.24. 如图,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)、如图1,当点 E 落在 CD 边上时,求线段 CE 的长;(2)、如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;(3)、在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.23. 某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为 元/件( ,且 是按0.5元的倍数上涨),当天销售利润为 元.(1)、求 与 的函数关系式(不要求写出自变量的取值范围);(2)、要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)、若每件文具的利润不超过 ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.24. 如图,在平面直角坐标系中,已知抛物线 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
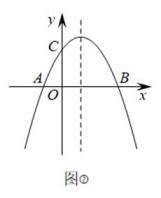 (1)、求该抛物线的解析式;(2)、如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;(3)、若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.