辽宁省锦州市黑山县2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入出卷网下载

一、选择题

1. 方程x²－3x+ $\frac{9}{4}$ ＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
2. 关于x的一元二次方程（a²﹣1）x²+x﹣2=0是一元二次方程，则a满足（　　）

A、a≠1 B、a≠﹣1 C、a≠±1 D、为任意实数

查看试题解析
3. 矩形具有而菱形不具有的性质是（）

A、两组对边分别平行且相等 B、两组对角分别相等 C、相邻两角互补 D、对角线相等

查看试题解析
4. 某种药品原价为36元/盒，经过连续两次降价后售价为25元/盒。设平均每次降价的百分率为 $x$ ，根据题意所列方程正确的是（）

A、 $36 {(1 - x)}^{2} = 36 - 25$ B、 $36 {(1 - 2 x)}^{2} = 25$ C、 $36 {(1 - x)}^{2} = 25$ D、 $25 (1 - x^{2}) = 36$

查看试题解析
5. 由下表：

$x$

6.17

6.18

6.19

6.20

$a x^{2} + b x + c$

$- 0.03$

$- 0.01$

0.04

0.1

可知方程 $a x^{2} + b x + c = 0$ （ $a \neq 0, a, b, c$ 为常数）一个根（精确到0.01）的范围是（）

A、 $6 < x < 6.17$ B、 $6.17 < x < 6.18$ C、 $6.18 < x < 6.19$ D、 $6.19 < x < 6.20$

查看试题解析
6. 菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是（6，0），点A的纵坐标是1，则点B的坐标是（）

A、（-3，﹣1） B、（3，﹣1） C、（3，1） D、（﹣1，3）

查看试题解析
7. 如图显示了用计算机模拟随机投掷一枚图钉的实验结果.随着试验次数的增加，“钉尖向上”的频率总在某个数字附近，显示出一定的稳定性，可以估计“钉尖向上”的概率是（）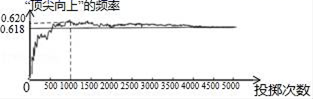

A、0.620 B、0.618 C、0.610 D、1000

查看试题解析
8. 如图，在菱形ABCD中，E是AB边上一点，且∠A=∠EDF=60°，有下列结论：①AE=BF；②△DEF是等边三角形；③△BEF是等腰三角形；④∠ADE=∠BEF，其中结论正确的个数是（）

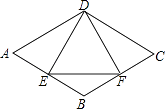A、3 B、4 C、1 D、2

查看试题解析

二、填空题

9. 方程（x+2）²=9的解是.

查看试题解析
10. 将一元二次方程（x-2）(2x-1)-x²=4化为一般形式是二次项系数是.

查看试题解析
11. 小明在一天晚上帮妈妈洗三个只有颜色不同的有盖茶杯，这时突然停电了，小明只好将茶杯和杯盖随机搭配在一起，那么三个茶杯颜色全部搭配正确的概率是.

查看试题解析
12. 关于x的一元二次方程ax²+bx+1＝0有两个相等的实数根，写出一组满足条件的实数a、b的值：a＝， b＝.

查看试题解析
13. 若关于x的一元二次方程x²+mx+2n=0有一个根是2，则m+n= ．

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，M，N分别是AB，AC的中点，延长BC至点D，使CD= $\frac{1}{2}$ BC，连接DM，DN，MN，若AB=6，则DN= ．

查看试题解析
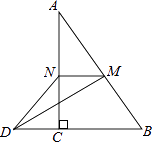15. 如图所示，直线a经过正方形ABCD的顶点A，分别过顶点D、B作DE⊥a于点E、BF⊥a于点F，若DE＝4，BF＝3，则EF的长为.

查看试题解析
16.
如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为．

查看试题解析

三、解答题

17. 解方程：(用适当的方法解方程)

(1)、解方程：x²﹣3x+2=0.

(2)、（2x-3）+2x（2x-3）=0

(3)、3x²=2－5x

查看试题解析
18. 如图，四边形ABCD是矩形，把矩形沿AC折叠，点B落在点E处，AE与DC的交点为O，连接DE．

(1)、求证：△ADE≌△CED；

(2)、求证：DE∥AC．

查看试题解析
19. 如图，矩形ABCD中，点P是线段AD上任意一点，点Q为BC上一点，且AP=CQ.

(1)、求证：BP=DQ；

(2)、若AB=4，且当PD=5时四边形PBQD为菱形.求AD为多少.

查看试题解析
20.
利用一面墙（墙的长度不限），另三边用58m长的篱笆围成一个面积为200m²的矩形场地，求矩形的长和宽．

查看试题解析
21. 某商场经销一种成本为每千克40元的水产品，经市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨价1元，月销售量就减少10千克．针对这种水产品的销售情况，请解答以下问题．

(1)、当销售单价定为每千克55元，计算月销售量和月销售利润；

(2)、商场计划在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？

查看试题解析
22. 有三张正面分别标有数字：﹣1，1，2的卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中抽出一张记下数字，放回洗匀后再从中随机抽出一张记下数字.

(1)、请用列表或画树状图的方法（只选其中一种），表示两次抽出卡片上的数字的所有结果；

(2)、将第一次抽出的数字作为点的横坐标x，第二次抽出的数字作为点的纵坐标y，求点（x，y）落在直线y=﹣x上的概率.

查看试题解析
23. 已知，正方形ABCD，G是BC边上ー点，连接AG，分别以AG和BG为直角边作等腰Rt△AGF和等腰Rt△GBE，使∠GBE＝∠AGF＝90°，点E，F在BC下方，连接EF.

求证：

(1)、∠BAG＝∠BGF，

(2)、CG＝EF：

查看试题解析
24. 已知，如图1，BD是边长为1的正方形ABCD的对角线，BE平分∠DBC交DC于点E，延长BC到点F，使CF=CE，连接DF，交BE的延长线于点G.

(1)、求证：△BCE≌△DCF；

(2)、求CF的长；

(3)、如图2，在AB上取一点H，且BH=CF，若以BC为x轴，AB为y轴建立直角坐标系，问在直线BD上是否存在点P，使得以B、H、P为顶点的三角形为等腰三角形？若存在，直接写出所有符合条件的P点坐标；若不存在，说明理由.

查看试题解析

$x$	6.17	6.18	6.19	6.20
$a x^{2} + b x + c$	$- 0.03$	$- 0.01$	0.04	0.1