辽宁省锦州黑山县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、单选题
-
1. 下列各组数中,互为相反数的是( )A、-2与 B、∣-2∣与 C、-2与 D、-2与2. 下列说法中,正确的是( )A、-4没有立方根 B、1的立方根是±1 C、-5的立方根 D、 的立方根是3. 生态园位于县城东北方向5千米处,如图中表示准确的是( )A、
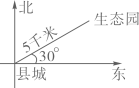 B、
B、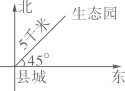 C、
C、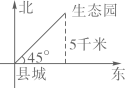 D、
D、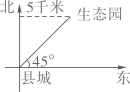 4. 面积为2的正方形的边长在( )
4. 面积为2的正方形的边长在( )
A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间5. 如图,是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )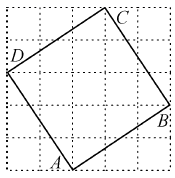 A、(2,3),(3,2) B、(3,2),(2,3) C、(2,3),(-3,2) D、(3,2),(-2,3)6. 下列根式是最简二次根式的是( )A、 B、 C、 D、7. 以直角三角形a、b、c为边,向外作半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )
A、(2,3),(3,2) B、(3,2),(2,3) C、(2,3),(-3,2) D、(3,2),(-2,3)6. 下列根式是最简二次根式的是( )A、 B、 C、 D、7. 以直角三角形a、b、c为边,向外作半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( )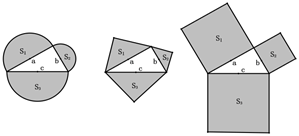 A、3 B、2 C、1 D、08. 如图,AD是△ABC的中线、∠ADC=45°,把△ADC沿着直线AD对折、点C落在点E的位置,如果BC=6,那么线段BE的长度的平方为( )
A、3 B、2 C、1 D、08. 如图,AD是△ABC的中线、∠ADC=45°,把△ADC沿着直线AD对折、点C落在点E的位置,如果BC=6,那么线段BE的长度的平方为( ) A、36 B、72 C、12 D、189. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、36 B、72 C、12 D、189. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、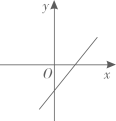 B、
B、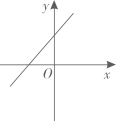 C、
C、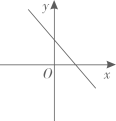 D、
D、 10. 在 ,﹣3.141, ,﹣0.5, ,0.5858858885…, 中无理数的个数有( )A、4 B、3 C、2 D、1
10. 在 ,﹣3.141, ,﹣0.5, ,0.5858858885…, 中无理数的个数有( )A、4 B、3 C、2 D、1二、填空题
-
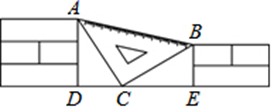
11. 2- 的绝对值为 , 相反数为.12. 若最简二次根式 与 能合并成一项,则a= .13. 在平面直角坐标系中,点A(0,-4)到x轴的距离为.14. 若已知 +(y+2)2=0,则(x+y)2019等于 .15. 课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间(如图), , ,从三角板的刻度可知 ,小聪很快就知道了砌墙砖块的厚度的平方(每块砖的厚度相等)为 2.
 16. 如图,长方形ABCD中AB=3,BC=4,且点A在坐标原点,(4,0)表示D点,那么C点的坐标为.
16. 如图,长方形ABCD中AB=3,BC=4,且点A在坐标原点,(4,0)表示D点,那么C点的坐标为.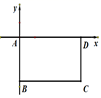 17. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .
17. 如图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若 , ,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是 .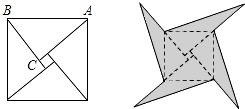 18. 如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶路程和时间,则这两人骑自行车的速度每小时相差km.
18. 如图,射线OA,BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s,t分别表示行驶路程和时间,则这两人骑自行车的速度每小时相差km.
三、解答题
-
19. 计算:(1)、(2)、(3)、(4)、 .20. 阅读下面计算过程:
请解决下列问题:
(1)、根据上面的规律,请直接写出 =;(2)、利用上面的解法,请化简:;
(3)、你能根据上面的知识化简 吗?若能,请写出化简过程.21. 如图所示,△BCO是△BAO经过折叠得到的.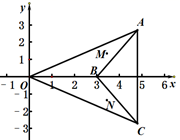 (1)、图中A与C的坐标之间的关系是什么?(2)、如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?22. 我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题:
(1)、图中A与C的坐标之间的关系是什么?(2)、如果△AOB中任意一点M的坐标为(x,y),那么它的对应点N的坐标是什么?22. 我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题: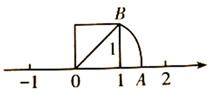 (1)、线段OA的长度是多少?(要求写出求解过程)(2)、这个图形的目的是为了说明什么?(3)、这种研究和解决问题的方式体现了_____的数学思想方法.(将下列符合的选项序号填在横线上)A、数形结合 B、代入 C、换元 D、归纳23. 张老师在一次“探究性学习”课中,设计了如下数表:
(1)、线段OA的长度是多少?(要求写出求解过程)(2)、这个图形的目的是为了说明什么?(3)、这种研究和解决问题的方式体现了_____的数学思想方法.(将下列符合的选项序号填在横线上)A、数形结合 B、代入 C、换元 D、归纳23. 张老师在一次“探究性学习”课中,设计了如下数表:n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)、请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= , b= , c=;
(2)、猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.24. 小王剪了两张直角三角形纸片,进行了如下的操作:操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
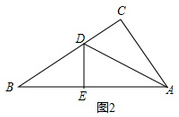
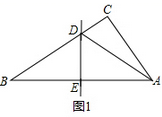 (1)、如果AC=6cm,BC=8cm,可求得△ACD的周长为;(2)、如果∠CAD:∠BAD=4:7,可求得∠B的度数为;(3)、操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
(1)、如果AC=6cm,BC=8cm,可求得△ACD的周长为;(2)、如果∠CAD:∠BAD=4:7,可求得∠B的度数为;(3)、操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
 25. 已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.(1)、求该函数的解析式,并画出它的图象;(2)、如果这条直线经过点P(m,2),求m的值;(3)、若O为坐标原点,求直线OP的解析式;(4)、求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
25. 已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.(1)、求该函数的解析式,并画出它的图象;(2)、如果这条直线经过点P(m,2),求m的值;(3)、若O为坐标原点,求直线OP的解析式;(4)、求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.