辽宁省鞍山市台安县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、单选题
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是( )A、诚 B、信 C、友 D、善2. 若实数m、n满足 ,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是 ( )A、12 B、10 C、8或10 D、63. 下列计算正确的是( )A、a3•a2=a6 B、a2+a4=2a2 C、(3a3)2=9a6 D、(3a2)3=9a64. 计算(﹣4x3+2x)÷2x的结果正确的是( )A、﹣2x2+1 B、2x2+1 C、﹣2x3+1 D、﹣8x4+2x5. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
 A、60° B、65° C、75° D、85°6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、60° B、65° C、75° D、85°6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( ) A、
A、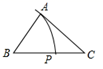 B、
B、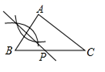 C、
C、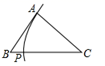 D、
D、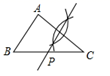 7. 如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( )
7. 如图,∠MON=30°,且OP平分∠MON,过点P作PQ∥OM交ON于点Q.若点P到OM的距离为2,则OQ的长为( ) A、1 B、2 C、3 D、48. 如图,等边△ABC的边长为4,AD是边BC上的中线,F是边AD上的动点,E是边AC上一点,若AE=2,则EF+CF取得最小值时,∠ECF的度数为( )
A、1 B、2 C、3 D、48. 如图,等边△ABC的边长为4,AD是边BC上的中线,F是边AD上的动点,E是边AC上一点,若AE=2,则EF+CF取得最小值时,∠ECF的度数为( ) A、15° B、22.5° C、30° D、45°
A、15° B、22.5° C、30° D、45°二、填空题
-
9. 在平面直角坐标系中,点 与点 关于 轴对称,则 的值是 .10. 一个凸多边形的内角和与外角和相等,它是边形.11. =.12. 已知ax=3,ay=9,则a2x+y=.13. 如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的角分线.若在边AB上截取BE=BC,连接DE,则图中共有个等腰三角形.
 14.
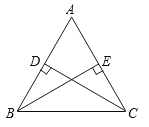
14.如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“”.
 15. 如图,AD平分∠BAC,要使△ABD≌△ACD,可添加条件.(添加一个即可)
15. 如图,AD平分∠BAC,要使△ABD≌△ACD,可添加条件.(添加一个即可) 16. 如图所示,在△ABC中,BD是AC边上的中线,BD⊥BC,∠ABC=120°,AB=8,则BC=.
16. 如图所示,在△ABC中,BD是AC边上的中线,BD⊥BC,∠ABC=120°,AB=8,则BC=.
三、解答题
-
17. 计算:(﹣3xy2)3+(﹣2x2y4)(﹣xy2)18. 化简求值:(a+1)(a+4)+a(a﹣4),其中a=﹣2.19. △ABC在平面直角坐标系中的位置如图所示.
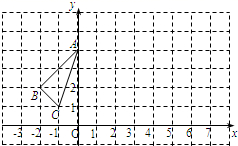
( 1 )画出△ABC关于y轴对称的△A1B1C1;
( 2 )将△ABC向右平移6个单位,作出平移后的△A2B2C2 , 并写出△A2B2C2各顶点的坐标;
( 3 )观察△A1B1C1和△A2B2C2 , 它们是否关于某条直线对称?若是,请在图上画出这条对称轴.
20. 如图, 中, ,小聪同学利用直尺和圆规完成了如下操作:①作 的平分线 交 于点 ;
②作边 的垂直平分线 , 与 相交于点 ;
③连接 , .
请你观察图形解答下列问题:
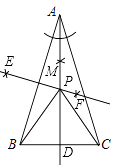 (1)、线段 , , 之间的数量关系是;(2)、若 ,求 的度数.21. 如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F.
(1)、线段 , , 之间的数量关系是;(2)、若 ,求 的度数.21. 如图,四边形ABCD的内角∠DCB与外角∠ABE的平分线相交于点F. (1)、若BF∥CD,∠ABC=80°,求∠DCB的度数;(2)、已知四边形ABCD中,∠A=105º,∠D=125º,求∠F的度数;(3)、猜想∠F、∠A、∠D之间的数量关系,并说明理由.22. 如图,在 中, , ,D是AB边上一点 点D与A,B不重合 ,连结CD,将线段CD绕点C按逆时针方向旋转 得到线段CE,连结DE交BC于点F,连接BE.
(1)、若BF∥CD,∠ABC=80°,求∠DCB的度数;(2)、已知四边形ABCD中,∠A=105º,∠D=125º,求∠F的度数;(3)、猜想∠F、∠A、∠D之间的数量关系,并说明理由.22. 如图,在 中, , ,D是AB边上一点 点D与A,B不重合 ,连结CD,将线段CD绕点C按逆时针方向旋转 得到线段CE,连结DE交BC于点F,连接BE. (1)、求证: ≌ ;
(1)、求证: ≌ ;