河南省周口市川汇区2020届九年级上学期数学期中考试试卷
试卷更新日期：2020-10-09 类型：期中考试
一、选择题
-
1. 若x＝1是方程x2+bx＝0的一个根，则它的两根之和是（ ）A、1 B、﹣1 C、0 D、±12. 已知关于x的一元二次方程（x﹣1）2+m＝0有实数根，则m的取值范围是（ ）A、m≥0 B、m≤0 C、m＞0 D、m＜03. 获2019年度诺贝尔化学奖的“锂电池”创造了一个更清洁的世界.我国新能源发展迅猛，某种特型锂电池2016年销售量为8万个，到2018年销售量为97万个.设年均增长率为x，可列方程为（ ）A、8（1+x）2＝97 B、97（1﹣x）2＝8 C、8（1+2x）＝97 D、8（1+x2）＝974. 已知抛物线y＝x2﹣2mx﹣1（m＞0）的顶点M关于坐标原点O的对称点为N，若点N在这条抛物线上，则点M的坐标为（ ）A、（﹣1，2） B、（1，﹣2） C、（﹣1，﹣2） D、（1，2）5. 已知点A（﹣1，5），B（0，0），C（4，0），D（2019，m），E（2020，n）在某二次函数的图象上.下列结论：①图象开口向上；②图象的对称轴是直线x＝2；③m＜n；④当0＜x＜4时，y＜0.其中正确的个数是（ ）A、1 B、2 C、3 D、46. 将抛物线y=x2向右平移2个单位，再向上平移1个单位，所得抛物线相应的函数表达式是（ ）A、y=（x+2）2+1 B、y=（x+2）2﹣1 C、y=（x﹣2）2+1 D、y=（x﹣2）2﹣17. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、菱形 B、等边三角形 C、矩形 D、圆8. 如图，在平面直角坐标系中，线段AB的端点在格点上，将AB绕点P旋转一定的角度，得到线段A′B′，则点P的坐标为（ ）
A、（﹣1，2） B、（1，﹣2） C、（﹣1，﹣2） D、（1，2）9. 如图，在△ABC中，∠ACB＝α，将△ABC绕点C顺时针方向旋转到△A′B′C的位置，使AA′∥BC，设旋转角为β，则α，β满足关系（ ）
A、α+β＝90° B、α+2β＝180° C、2α+β＝180° D、α+β＝180°10. 如图，已知二次函数y＝ax2+bx+c（a≠0）的图象.下列结论：①b＞0；②a﹣b+c＜0；③ax2+bx+c＝1有两个实数根.其中正确的个数是（ ）
A、0 B、1 C、2 D、3二、填空题
-
11. 直线y＝2被抛物线y＝x2﹣3x+2截得的线段长为.12. 关于x的方程mx2+mx+1=0有两个相等的实数根，那么m=.13. 如图，BD是⊙O的直径，弦AC平分∠BCD，若四边形ABCD的面积为2，则AC＝.
14. 如图，经过抛物线y＝x2+x﹣2与坐标轴交点的圆与抛物线另交于点D，与y轴另交于点E，则∠BED＝ ．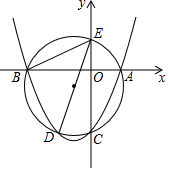
15. 如图，在正方形ABCD中，AB＝4，点E是BC上的一个动点，将△CDE绕着点E逆时针旋转90°，得到△C′D′E，则A，D′两点距离的最小值等于.
三、解答题
-
16. 按要求解方程：(1)、用配方法解6x2+x﹣2＝0；(2)、在解方程x2﹣2x＝2﹣x时，某同学的解答如下，请你指出解答中出现的错误，并给出正确解题过程.
17. 已知关于x的一元二次方程x2﹣（2a﹣1）x+a2+2＝0有两个不相等的实数根.(1)、求实数a的取值范围，并求a的最大整数；(2)、x＝1可能是方程的一个根吗？若是，请求出它的另一个根，若不是，请说明理由.18. 已知二次函数y＝﹣x2+2x+3.
(1)、在下面的直角坐标系中画出函数的图象；(2)、写出函数的3条性质.19. 如图，是一块三角形材料，∠A＝30°，∠C＝90°，AB＝6.用这块材料剪出一个矩形DECF，点D，E，F分别在AB，BC，AC上，要使剪出的矩形DECF面积最大，点D应该选在何处？
20. 如图，求作△ABC绕某点旋转一定角度后的△A′B′C′时，某同学只作了一部分图形.
(1)、请把△A′B′C′作完整，并保留作图痕迹；(2)、写出基本作图步骤.21. 如图，是一张盾构隧道断面结构图.隧道内部为以O为圆心，AB为直径的圆.隧道内部共分为三层，上层为排烟道，中间为行车隧道，下层为服务层.点A到顶棚的距离为1.6m，顶棚到路面的距离是6.4m，点B到路面的距离为4.0m.请求出路面CD的宽度.（精确到0.1m）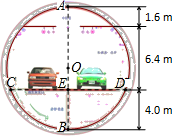
22. 在△ABC中，AC＝BC，∠ACB＝90°.点P在是平面内不与点A，B，C重合的任意一点，连接PC，将线段PC绕点C顺时针旋转90°得到线段DC，连接AD，BP.
(1)、观察猜想当点P在直线AC上时，如图1，线段BP与AD的数量关系是 ， 直线BP与直线AD的位置关系是；
(2)、拓展探究当点P不在直线AC上时，（1）中的数量关系和位置关系还成立吗？并就图2的情形说明理由；
(3)、解决问题若点M，N分别是AB和AC的中点，点P在直线MN上，请直接写出点A，P，D在同一条直线上时 的值.
23. 如图，在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（3，0），B（﹣1，0），与y轴交于点C.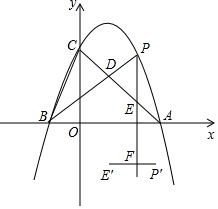
(1)、求抛物线的解析式；(2)、点P是直线AC上方的抛物线上一动点（异于点A、C），连接BC，AC，PA，PB，PB与AC交于点D，设点P的横坐标为m.①若△CBD，△DAP的面积分别为S1和S2 ， 当S1﹣S2最小时，求点P的坐标；
②过点P作x轴的垂线，交AC于点E.以原点O为旋转中心，将线段PE顺时针旋转90°，得到线段P′E′.当线段P′E′与直线PE有交点时，设交点为F，求交点F的路径长.