河南省郑州市高新区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 两个人的影子在两个相反的方向,这说明( )A、他们站在阳光下 B、他们站在路灯下 C、他们站在路灯的两侧 D、他们站在月光下2. 已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是( )A、l B、2.25 C、4 D、23. 在一个不透明的布袋中装有40个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到黄球的频率稳定在0.30左右,则布袋中黄球可能有( )A、12个 B、14个 C、18个 D、28个4. 如图,王华用橡皮泥做了个圆柱,再用手工刀切去一部分,则其左视图是( )
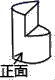 A、
A、 B、
B、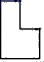 C、
C、 D、
D、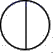 5. 若 ,则 ( )A、 B、 C、 D、6. 已知点 把线段 分成两条线段 、 ,且 ,下列说法错误的是( )A、如果 ,那么线段 被点 黄金分割 B、如果 ,那么线段 被点 黄金分割 C、如果线段 被点 黄金分割,那么 与 的比叫做黄金比 D、 是黄金比的近似值7. 已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为( )A、5 B、﹣1 C、2 D、﹣58. 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )
5. 若 ,则 ( )A、 B、 C、 D、6. 已知点 把线段 分成两条线段 、 ,且 ,下列说法错误的是( )A、如果 ,那么线段 被点 黄金分割 B、如果 ,那么线段 被点 黄金分割 C、如果线段 被点 黄金分割,那么 与 的比叫做黄金比 D、 是黄金比的近似值7. 已知关于x的方程x2+3x+a=0有一个根为﹣2,则另一个根为( )A、5 B、﹣1 C、2 D、﹣58. 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )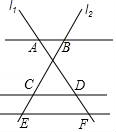 A、 B、 C、 D、9. 如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于 AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A、 B、 C、 D、9. 如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于 AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )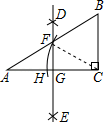 A、 B、2 C、 +1 D、2 ﹣210. 如图,已知矩形 中,点 是边 上的任一点,连接 ,过 作 的垂线交 延长线于点 ,交边 于点 ,则图中共有相似三角形( )
A、 B、2 C、 +1 D、2 ﹣210. 如图,已知矩形 中,点 是边 上的任一点,连接 ,过 作 的垂线交 延长线于点 ,交边 于点 ,则图中共有相似三角形( )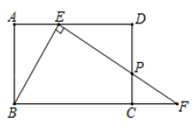 A、6对 B、5对 C、4对 D、3对11. 如图,在矩形ABCD中,M是BC边上一点,连接AM, 过点D作 ,垂足为 若 , ,则BM的长为
A、6对 B、5对 C、4对 D、3对11. 如图,在矩形ABCD中,M是BC边上一点,连接AM, 过点D作 ,垂足为 若 , ,则BM的长为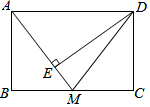 A、1 B、 C、 D、12. 如图,四边形 是边长为6的正方形,点 在边 上, ,过点 作 ,分别交 于 两点.若 分别是 的中点,则 的长为( )
A、1 B、 C、 D、12. 如图,四边形 是边长为6的正方形,点 在边 上, ,过点 作 ,分别交 于 两点.若 分别是 的中点,则 的长为( )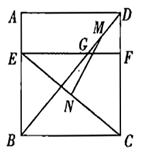 A、3 B、 C、 D、4
A、3 B、 C、 D、4二、填空题
-
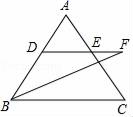
13. 已知: 是反比例函数,则m= .14. 若菱形的两条对角线长分别是方程 的两实根,则菱形的面积为.15. 关于x的一元二次方程 有实数根,则实数a满足的条件是.16. 如图,在△ABC中,DE∥BC,BF平分∠ABC,交DE的延长线于点F,若AD=1,BD=2,BC=4,则EF=.
 17. 如图,平面直角坐标系 中,已知 和B点 ,点C是 的中点,点P在x轴上,若以P、A、C为顶点的三角形与 相似,那么点P的坐标是.
17. 如图,平面直角坐标系 中,已知 和B点 ,点C是 的中点,点P在x轴上,若以P、A、C为顶点的三角形与 相似,那么点P的坐标是.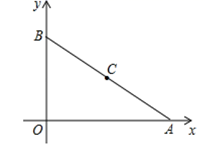 18. 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2 ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为.
18. 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2 ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为.
三、解答题
-
19. 校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
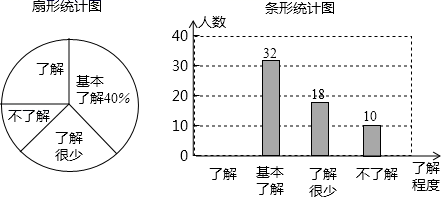 (1)、在这次活动中抽查了多少名中学生?(2)、若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.(3)、若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.20. 如图,已知点 是坐标原点, 两点的坐标分别为 , .
(1)、在这次活动中抽查了多少名中学生?(2)、若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.(3)、若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.20. 如图,已知点 是坐标原点, 两点的坐标分别为 , .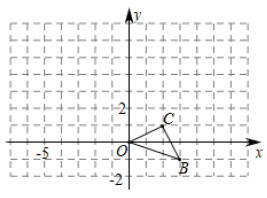 (1)、以 点为位似中心在 轴的左侧将 放大到原图的2倍(即新图与原图的相似比为2),画出对应的 ;(2)、若 内部一点 的坐标为 ,则点 对应点 的坐标是;(3)、求出变化后 的面积 .21. 已知关于 的一元二次方程 .
(1)、以 点为位似中心在 轴的左侧将 放大到原图的2倍(即新图与原图的相似比为2),画出对应的 ;(2)、若 内部一点 的坐标为 ,则点 对应点 的坐标是;(3)、求出变化后 的面积 .21. 已知关于 的一元二次方程 .求证:
(1)、方程总有两个不相等的实数根.(2)、若等腰 的两边 的长是这个方程的两个实数根,第三边 的长为5. 求 的周长.22. 《铁血红安》在中央一台热播后,吸引了众多游客前往影视基地游玩. 某天小明站在地面上给站在城楼上的小亮照相时发现:他的眼睛、凉亭顶端、小亮头顶三点恰好在一条直线上(如图). 已知小明的眼睛离地面1. 65米,凉亭顶端离地面2米,小明到凉亭的距离为2米,凉亭离城楼底部的距离为40米,小亮身高1. 7米. 请根据以上数据求出城楼的高度.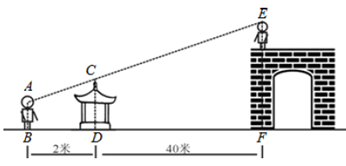 .23. 某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.(1)、当租金提高多少元时,公司的每日收益可达到10120元?(2)、汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益-维护费)24. 已知:如图,在平行四边形 中,G、H分别是 、 的中点,E、O、F分别是对角线 上的四等分点,顺次连接G、E、H、F.
.23. 某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.(1)、当租金提高多少元时,公司的每日收益可达到10120元?(2)、汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益-维护费)24. 已知:如图,在平行四边形 中,G、H分别是 、 的中点,E、O、F分别是对角线 上的四等分点,顺次连接G、E、H、F.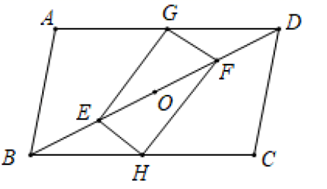 (1)、求证:四边形 是平行四边形;(2)、当平行四边形 满足条件时,四边形 是菱形;(3)、若 ,探究四边形 的形状,并说明理由.25. 如图
(1)、求证:四边形 是平行四边形;(2)、当平行四边形 满足条件时,四边形 是菱形;(3)、若 ,探究四边形 的形状,并说明理由.25. 如图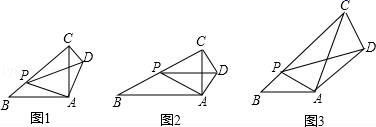 (1)、问题发现
(1)、问题发现如图1,在Rt△ABC中,∠A=90°, =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
①求 的值;②求∠ACD的度数.
(2)、拓展探究如图 2,在Rt△ABC中,∠A=90°, =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
(3)、解决问题如图 3,在△ABC中,∠B=45°,AB=4 ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.