河南省新乡市卫辉市2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 一元二次方程2x2﹣x﹣3=0的二次项系数、一次项系数、常数项分别是( )A、2,1,3 B、2,1,﹣3 C、2,﹣1,3 D、2,﹣1,﹣32. 二次根式: ; ; ; 中,能与 合并的是A、 和 B、 和 C、 和 D、 和3. 下列计算正确的是( )A、 B、 C、 D、4. 将方程x2﹣6x+2=0配方后,原方程变形为( )A、(x+3)2=﹣2 B、(x﹣3)2=﹣2 C、(x﹣3)2=7 D、(x+3)2=75. 如图,四边形ABCD和A′B′C′D′是以点O为位似中心的位似图形,若OA:OA′=2:3,则四边形ABCD与四边形A′B′C′D′的面积比为( )
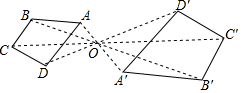 A、4:9 B、2:5 C、2:3 D、 :6. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A、4:9 B、2:5 C、2:3 D、 :6. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )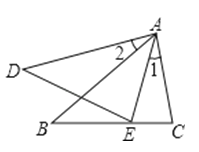 A、= B、= C、∠B=∠D D、∠C=∠AED7. 如图, 是 的中位线,已知 的面积为12,则四边形 的面积为( ).
A、= B、= C、∠B=∠D D、∠C=∠AED7. 如图, 是 的中位线,已知 的面积为12,则四边形 的面积为( ). A、3 B、6 C、9 D、108.
A、3 B、6 C、9 D、108.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为xm,则下面所列方程正确的是( )
 A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5709. 如图,已知AB、CD、EF互相平行,且AB=1,CD=4,那么EF的长是( )
A、(32﹣2x)(20﹣x)=570 B、32x+2×20x=32×20﹣570 C、(32﹣x)(20﹣x)=32×20﹣570 D、32x+2×20x﹣2x2=5709. 如图,已知AB、CD、EF互相平行,且AB=1,CD=4,那么EF的长是( ) A、 B、 C、 D、10. 如图,在矩形AOBC中,点A的坐标为(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )
A、 B、 C、 D、10. 如图,在矩形AOBC中,点A的坐标为(-2,1),点C的纵坐标是4,则B,C两点的坐标分别是( )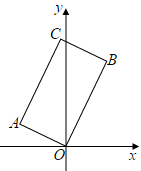 A、( , ),( , ) B、( , ),( , ) C、( , ),( , ) D、( , ),( , )
A、( , ),( , ) B、( , ),( , ) C、( , ),( , ) D、( , ),( , )二、填空题
-
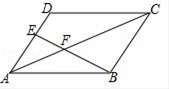
11. 若代数式 有意义,则m的取值范围是.12. 若 ,则 = .13. 已知等腰三角形的两边长是方程x2﹣9x+18=0的两个根,则该等腰三角形的周长为.14. 如图,在▱ABCD中,E为AD的三等分点,AE= AD,连结BE,交AC于点F,AC=15,则AF为.
 15. 将三角形纸片( )按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 ,已知 , ,若以点 , , 为顶点的三角形与 相似,那么 的长是.
15. 将三角形纸片( )按如图所示的方式折叠,使点 落在边 上,记为点 ,折痕为 ,已知 , ,若以点 , , 为顶点的三角形与 相似,那么 的长是.
三、解答题
-
16. 计算:(1)、(2)、(3)、17. 解方程:(1)、(2x-1)2-25=0(2)、(3)、18. 如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
 (1)、△ABE与△ADF相似吗?请说明理由.(2)、若AB=6,AD=12,BE=8,求DF的长.19. 如图,在边长为1的正方形网格内有一个三角形 .
(1)、△ABE与△ADF相似吗?请说明理由.(2)、若AB=6,AD=12,BE=8,求DF的长.19. 如图,在边长为1的正方形网格内有一个三角形 .
( 1 )把 沿着 轴向右平移5个单位得到 ,请你画出 ;
( 2 )请你以 点为位似中心在第一象限内画出 的位似图形 ,使得 与 的位似比为 ;
( 3 )请你写出 三个顶点的坐标.
20. 已知关于x的方程x2﹣(2k+1)x+4(k﹣ )=0(1)、求证:无论k取何值,这个方程总有实数根;(2)、若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.21. 某商业街有店面房共100间,2015年平均每间店面房的年租金为1万元,由于物价上涨,到2017年平均每间店面房的年租金上涨到了1.21万元,据预测,当每间的年租金定为12100元时,可全部租出;若每间的年租金每增加0.1万元,就要少租出10间,该商业街管委会要为租出的商铺每间每年交各种费用0.1万元,未租出的商铺每间每年交各种费用0.05万元.(1)、求2015年至2017年平均每间店面房年租金的平均增长率;(2)、当每间店面房的年租金上涨多少万元时,该商业街的年收益(收益=租金﹣各种费用)为103.8万元?22. 如图
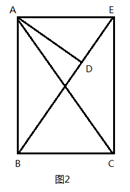
 (1)、观察发现:如图1,在 中, ,点 在边 上,过 作 交 于 , , , .填空:
(1)、观察发现:如图1,在 中, ,点 在边 上,过 作 交 于 , , , .填空:① 与 是否相似(直接回答);
② ; ;
(2)、拓展探究:将 绕顶点 旋转到图2所示的位置,猜想 与 是否相似?若不相似,说明理由;若相似,请证明;(3)、迁移应用:将 绕顶点 旋转到点 、 、 在同一条直线上时,直接写出线段 的长.23. 已知:如图,在平面直角坐标系中, 是直角三角形, ,点 、 的横坐标是一元二次方程 的两根( ),直线 与 轴交于 , 点的坐标为 .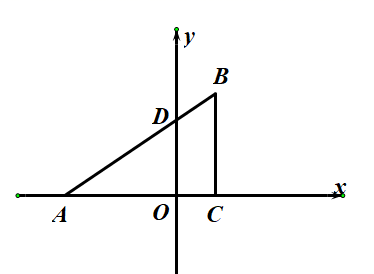 (1)、求直线 的函数表达式;(2)、在 轴上找一点 ,连接 ,使得以点 、 、 为顶点的三角形与 相似(不包括全等),并求点 的坐标;(3)、在(2)的条件下,点 、 分别是 和 上的动点,连接 ,点 、 分别从 、 同时出发,以每秒1个单位长度的速度运动,当点 到达点 时,两点停止运动,设运动时间为 秒,请直接写出几秒时以点 、 、 为顶点的三角形与 相似.
(1)、求直线 的函数表达式;(2)、在 轴上找一点 ,连接 ,使得以点 、 、 为顶点的三角形与 相似(不包括全等),并求点 的坐标;(3)、在(2)的条件下,点 、 分别是 和 上的动点,连接 ,点 、 分别从 、 同时出发,以每秒1个单位长度的速度运动,当点 到达点 时,两点停止运动,设运动时间为 秒,请直接写出几秒时以点 、 、 为顶点的三角形与 相似.