河南省三门峡市陕州区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 若关于x的方程 是一元二次方程,则m的取值范围是( )A、 . B、 . C、 D、 .2. 抛物线 的顶点坐标为( )A、(-2, 2) B、(2, -2) C、(2, 2) D、(-2, -2)3. 要得到抛物线y=2(x+4)2﹣1,可以将抛物线y=2x2( )A、向左平移4个单位,再向上平移1个单位 B、向左平移4个单位,再向下平移1个单位 C、向右平移4个单位,再向上平移1个单位 D、向右平移4个单位,再向下平移1个单位4. 将下图所示的图案以圆心为中心,旋转180°后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、246. 在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )A、点A在圆外 B、点A在圆内 C、点A在圆上 D、无法确定7. 如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2 , 设小路的宽为xm,那么x满足的方程是( )
5. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、246. 在△ABC中,∠C=90°,以点B为圆心,以BC长为半径作圆,点A与该圆的位置关系为( )A、点A在圆外 B、点A在圆内 C、点A在圆上 D、无法确定7. 如图,某小区规划在一个长16m,宽9m的矩形场地ABCD上,修建同样宽的小路,使其中两条与AB平行,另一条与AD平行,其余部分种草,如果使草坪部分的总面积为112m2 , 设小路的宽为xm,那么x满足的方程是( ) A、2x2-25x+16=0 B、x2-25x+32=0 C、x2-17x+16=0 D、x2-17x-16=08. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、
A、2x2-25x+16=0 B、x2-25x+32=0 C、x2-17x+16=0 D、x2-17x-16=08. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、 B、
B、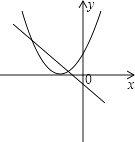 C、
C、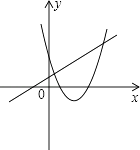 D、
D、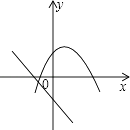 9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( )
9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( ) A、点A B、点B C、点C D、点D10. 如图,⊙O的半径为2,点A的坐标为 ,直线AB为⊙O的切线,B为切点,则B点的坐标为( )
A、点A B、点B C、点C D、点D10. 如图,⊙O的半径为2,点A的坐标为 ,直线AB为⊙O的切线,B为切点,则B点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程5x2﹣x﹣3=x2﹣3+x的二次项是 , 二次项系数是 , 一次项系数是 , 常数项是.12. 函数y=(m+1)x|m|+1+5x﹣5是二次函数,则m=.13. 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1= , DE=.
 14. 如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=.
14. 如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=. 15. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
15. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c=0;④当y>0时,x的取值范围是﹣1≤x<3;⑤当x<0时,y随x增大而增大.
其中结论正确的是(只需填序号)
三、解答题
-
16. 解方程(1)、x2﹣2x﹣3=0(2)、(x﹣3)2+4x(x﹣3)=0.17. 已知△ABC内接于以AB为直径的⊙O , 过点C作⊙O的切线交BA的延长线于点D , 且DA∶AB=1∶2.
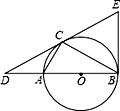 (1)、求∠CDB的度数;(2)、在切线DC上截取CE=CD , 连接EB , 判断直线EB与⊙O的位置关系,并证明.18. 求证:无论p取何值,方程(x﹣3)(x﹣2)﹣p2=0总有两个不等的实数根.19. 如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:
(1)、求∠CDB的度数;(2)、在切线DC上截取CE=CD , 连接EB , 判断直线EB与⊙O的位置关系,并证明.18. 求证:无论p取何值,方程(x﹣3)(x﹣2)﹣p2=0总有两个不等的实数根.19. 如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明: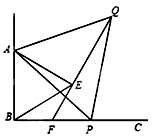 (1)、△ABP≌△AEQ;(2)、EF=BF20. 某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)(1)、公司每日租出x辆车时,每辆车的日租金为元(用含x的代数式表示);(2)、当每日租出多少辆时,租赁公司日收益最大?最大是多少元?(3)、当每日租出多少辆时,租赁公司的日收益不盈也不亏?21. 已知△ABC的三个顶点的坐标分别为 , , .
(1)、△ABP≌△AEQ;(2)、EF=BF20. 某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出)(1)、公司每日租出x辆车时,每辆车的日租金为元(用含x的代数式表示);(2)、当每日租出多少辆时,租赁公司日收益最大?最大是多少元?(3)、当每日租出多少辆时,租赁公司的日收益不盈也不亏?21. 已知△ABC的三个顶点的坐标分别为 , , .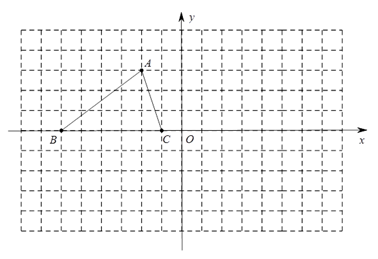 (1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.22. 车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.
(1)、点A关于y轴对称的点的坐标是;(2)、将△ABC绕坐标原点O顺时针旋转180°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.22. 车辆转弯时,能否顺利通过直角弯道的标准是:车辆是否可以行使到和路的边界夹角是45°的位置(如图1中②的位置),例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,则车辆就能通过.

 (1)、试说明长8m,宽3m的消防车不能通过该直角转弯;(2)、为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.23. 如图,对称轴为直线 的抛物线 与x轴相交于A、B两点,其中A点的坐标为(-3,0).
(1)、试说明长8m,宽3m的消防车不能通过该直角转弯;(2)、为了能使长8m,宽3m的消防车通过该弯道,可以将转弯处改为圆弧(分别是以O为圆心,以OM和ON为半径的弧),具体方案如图3,其中OM⊥OM′,请你求出ON的最小值.23. 如图,对称轴为直线 的抛物线 与x轴相交于A、B两点,其中A点的坐标为(-3,0). (1)、求点B的坐标;(2)、已知 ,C为抛物线与y轴的交点.
(1)、求点B的坐标;(2)、已知 ,C为抛物线与y轴的交点.①若点P在抛物线上,且 ,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.