河南省平顶山市教研联盟2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入出卷网下载

一、选择题

1. 下列方程是一元二次方程的是（）

A、2（x﹣1）＝4 B、 $x^{2} + \frac{1}{x} = 2$ C、 $2 x^{2} + 3 x + 1 = 0$ D、x+y＝0

查看试题解析
2. 若 $\frac{a}{b} = \frac{c}{d} = \frac{1}{3}$ （b+d≠0），则 $\frac{a + c}{b + d}$ 的值为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、1 D、 $\frac{4}{3}$

查看试题解析
3. 下列方程有两个不相等的实数根的是（）

A、 $x^{2} + 6 x - 5 = 0$ B、 $3 x^{2} + 6 x + 5 = 0$ C、 $x^{2} + 4 x + 4 = 0$ D、 $x^{2} + 2 x + 1 = 0$

查看试题解析
4. 下列可以判断是菱形的是（）

A、一组对边平行且相等的四边形 B、对角线相等的平行四边形 C、对角线垂直的四边形 D、对角线互相垂直且平分的四边形

查看试题解析
5. 王师傅的蘑菇培育基地2017年产量是60吨，由于科学管理，产量逐年增加，2019年产量达到80吨如果每年的增长率相同，设增长率为x，那么可列方程（）

A、 $60 {(1 + x)}^{2} = 80$ B、 $80 {(1 - x)}^{2} = 60$ C、 $60 {(1 + 2 x)}^{2} = 80$ D、 $60 (1 + x) + 60 {(1 + x)}^{2} = 140$

查看试题解析
6. 如图，在△ABC中，点D是AB边上一点（不与A，B两点重合），下列条件：①∠ACD＝∠B； ②∠ADC＝∠ACB；③AC²＝AD•AB；④ $\frac{A C}{B C} = \frac{A D}{C D}$ ，能使△ABC∽△ACD的条件的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 在一个不透明的盒子里装有只有颜色不同的10个红球和若中个黄球每次从盒子里摸出一个球，记录下颜色后再放回，经过多次重复试验，发现摸到黄球的频率稳定在0.8.请估计盒子里黄球约有（）

A、20个 B、40个 C、60个 D、80个

查看试题解析
8. 顶角为36°的等腰三角形我们把这种三角形称为“黄金三角形”，它的底与腰的比值为 $\frac{\sqrt{5} - 1}{2}$ .如图，在△ABC中，∠A＝36°，AB＝AC，BD平分∠ABC交AC于点D，若CD＝1，则AC的长为（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、 $\frac{\sqrt{5} + 2}{2}$ D、 $\frac{\sqrt{5} + 3}{2}$

查看试题解析
9. 如图，菱形ABCD沿对角线AC的方向平移到菱形A'B′C′D′的位置，点A′恰好是AC的中点.若菱形ABCD的边长为2，∠BCD＝60°，则阴影部分的面积为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\sqrt{3}$

查看试题解析
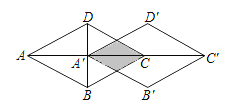10. 如图，在平面直角坐标系xOy中，矩形OABC的边O在x轴上，OC在y轴上，OA＝6，OC＝4，PC＝ $\frac{1}{3}$ BC.将矩形OABC绕点O以每秒45°的速度沿顺时针方向旋转，则第2019秒时，点P的坐标为（）

A、（3 $\sqrt{2}$ ， $\sqrt{2}$ ） B、（2，﹣1） C、（ $\sqrt{2}$ ，﹣3 $\sqrt{2}$ ） D、（﹣1，2）

查看试题解析

二、填空题

11. 为了检验某批足球的质量，随机抽取了100个足球，发现合格的有90个.如果从这批足球中随机取出一个，那么这个足球合格的概率约为.

查看试题解析
12. 若关于x的方程kx²+（2k﹣1）x+k﹣2＝0有两个相等的实数根，则k的值为.

查看试题解析
13. 如图，E、F分别为矩形ABCD的边AD，BC的中点.若矩形ABCD与矩形EABF相似，AB＝6，则AD的长为.

查看试题解析
14. 中国古代三国时期的数学家赵爽，创作了一幅“勾股弦方图”，通过数形结合，给出了勾股定理的详细证明如图，在“勾股弦方图”中，以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成，这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”，若正方形ABCD与正方形EFCH的面积分别为169和49，则所用细塑料棒的长度为.

查看试题解析
15. 如图，在矩形ABCD中，AB＝3，AD＝4，点E是AD边上一动点，将△ABE沿BE折叠，使点A的对应点A′恰好落在矩形ABCD的对角线上，则AE的长为.

查看试题解析

三、解答题

16. 解下列方程

(1)、x²+x＝0.

(2)、2x²+4x﹣1＝0.

查看试题解析
17. 如图，在△ABC中，点D是AB的中点，DE∥BC交AC于点E，DF∥BE交AC于点F，若EF＝3，求AC的长.

查看试题解析
18. 如图，在正方形ABCD的上方作等边三角形ADE，连接BE，CE.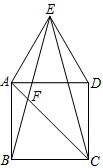

(1)、求证：△ABE≌△DCE；

(2)、连接AC，设AC与BE交于点F，求∠BFC的度数.

查看试题解析
19. 课堂上，蒋老师拿出了4张分别与有数字1，2，3，4的卡片（除数字外其他都相同），让同学们随机抽取两张，并计算这两张卡片上数字的和.

(1)、请用列表或画树状图的方法列举出所有等可能的结果；

(2)、求两张卡片上数字的和大于5的概率.

查看试题解析
20. 某商场新上市一款毛衣，进价是40元，当售价为80元，一天可以销售20件.若售价每降价1元，则每天可以多卖2件.设售价为x元，当天的销售量为y件.

(1)、销售量y与售价x之间的函数表达式为；

(2)、在尽可能增大销售量的前提下，问这款毛衣降价后的售价为多少元时，商场当天可获利1200元？

查看试题解析
21. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝6，点E是斜边AB上的一个动点，连接CE，过点B，C分别作BD∥CE，CD∥BE，BD与CD相交于点D.

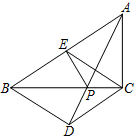(1)、当CE⊥AB时，求证：四边形BECD是矩形；

(2)、填空：
①当BE的长为时，四边形BECD是菱形；

②在①的结论下，若点P是BC上一动点，连接AP，EP，则AP+EP的最小值为.

查看试题解析
22. 正方形ABCD与正方形DEFG按如图1放置，点A，D，G在同一条直线上，点E在CD边上，AD＝3，DE＝ $\sqrt{2}$ ，连接AE，CG

(1)、线段AE与CC的关系为；

(2)、将正方形DEFG绕点D顺时针旋转一个锐角后，如图2，请问（1）中的结论是否仍然成立？请说明理由

(3)、在正方形DEFG绕点D顺时针旋转一周的过程中，当∠AEC＝90°时，请直接写出AE的长.

查看试题解析
23. 如图在平面直角坐标系xOy中，直线y＝﹣ $\frac{3}{4}$ x+6与x轴、y轴分别交于B、A两点，点P从点A开沿y轴以每秒1个单位长度的速度向点O运动，点Q从点A开始沿AB向点B运动（当P，Q两点其中一点到达终点时，另一点也随之停止运动）如果点P，Q从点A同时出发，设运动时间为t秒.

(1)、如果点Q的速度为每秒 $\frac{3}{5}$ 个单位长度，那么当t＝5时，求证：△APQ∽△ABO；

(2)、如果点Q的速度为每秒2个单位长度，那么多少秒时，△APQ的面积为16？

(3)、若点H为平面内任意一点，当t＝4时，以点A，P，H，Q四点为顶点的四边形是矩形，请直接写出此时点H的坐标.

查看试题解析