河南省商丘市梁园区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 下列长度的三条线段,能组成三角形的是( )A、4,5,9 B、6,7,14 C、4,6,10 D、8,8,15
-
2. 下列平面图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
3. 点(1,﹣3)关于x轴对称点为( )A、(1,3) B、(﹣3,1) C、(3,1) D、(﹣1,3)
-
4. 有下列说法:①两个三角形全等,它们的形状一定相同;②两个三角形形状相同,它们一定是全等三角形;③两个三角形全等,它们的面积一定相等;④两个三角形面积相等,它们一定是全等三角形.其中正确的说法是( )A、①② B、②③ C、①③ D、②④
-
5. 根据下列条件不能唯一画出△ABC的是( )A、AB=5,BC=6,AC=7 B、AB=5,BC=6,∠B=45° C、AB= 5,AC=4,∠C=90° D、AB=5,AC=4,∠C=45°
-
6. 如图,已知△ABO≌△CDO,则下列结论不正确的是( )
 A、AB=OD B、∠A=∠C C、AD=BC D、∠AOB=∠COD
A、AB=OD B、∠A=∠C C、AD=BC D、∠AOB=∠COD -
7. 一个多边形的内角和与外角和相等,则这个多边形的边数为( )A、8 B、6 C、5 D、4
-
8. 如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
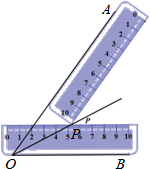 A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确
A、角平分线上的点到这个角两边的距离相等 B、角的内部到角的两边的距离相等的点在角的平分线上 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确 -
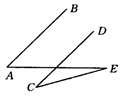
9. 如图, , ,则 等于( )
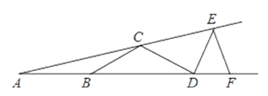 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 在四边形ABCD中∠C=55°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△EAF周长最小时,∠EAF的度数为( )
 A、55° B、70° C、125° D、110°
A、55° B、70° C、125° D、110°
二、填空题
-
11. 如图1所示,AB∥CD,∠A=45°,∠C=29°,则∠E=.
-
12. 如图, ,请你添加一个条件: , 使 (只添一个即可).
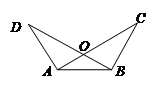
-
13. 某多边形内角和与外角和共1080°,则这个多边形的边数是.
-
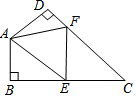
14. 如图,已知等边三角形ABC的高为7cm,P为△ABC内一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F.则PD+PE+PF=.
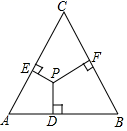
-
15. 如图,在 中,点A的坐标为 ,点B的坐标为 ,点C的坐标为 ,点D在第二象限,且 与 全等,点D的坐标是.
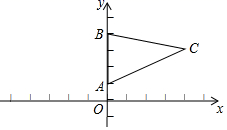
三、解答题
-
16. 如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=75°,∠C=45°,求∠DAE与∠AEC的度数.
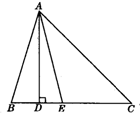
-
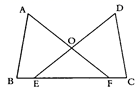
17. 已知:如图,B、E、F、C四点在同一条直线上,AB=DC,BE=CF,∠B=∠C.
求证:∠A=∠D.
-
18. 如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
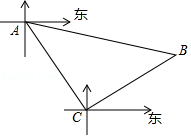 (1)、求此时货轮到小岛B的距离.(2)、在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.
(1)、求此时货轮到小岛B的距离.(2)、在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由. -
19. 如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
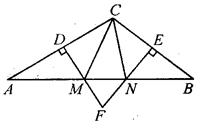 (1)、若△CMN的周长为15cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数.
(1)、若△CMN的周长为15cm,求AB的长;(2)、若∠MFN=70°,求∠MCN的度数. -
20. 如图,在平面直角坐标系中, 的顶点坐标分别为A(2,3)、B (1,1)、C(2,1)

( 1 )画出 关于 轴对称的 ,并写出点 的坐标为_▲_.
( 2 )将 向左平移4个单位长度得到 ,直接写出点 的坐标为_▲_.
( 3 )直接写出点B关于直线n(直线n上各点的纵坐标都为-1)对称点B'的坐标为_▲_.
( 4 )在 轴上找一点P,使PA+PB的值最小,标出P点的位置(保留画图痕迹)
-
21. 已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F.
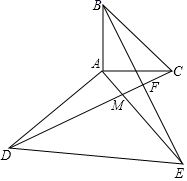 (1)、求证:△DAC≌△EAB.(2)、求证:CD⊥BE.
(1)、求证:△DAC≌△EAB.(2)、求证:CD⊥BE. -
22. 如图1,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
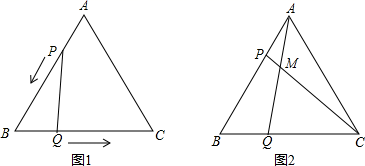 (1)、当运动时间为t秒时,BQ的长为厘米,BP的长为厘米.(用含t的式子表示)(2)、当t为何值时,△PBQ是直角三角形.(3)、如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
(1)、当运动时间为t秒时,BQ的长为厘米,BP的长为厘米.(用含t的式子表示)(2)、当t为何值时,△PBQ是直角三角形.(3)、如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数. -
23. 如图
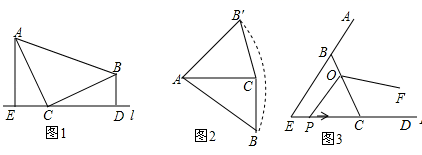 (1)、观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=2,将斜边AB绕点A逆时针旋转90°至AB',连接B′C,求△AB′C的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上且OC=2cm,动点P从点E沿射线EC以lcm/s速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF,设点P运动的时间为t秒.
(1)、观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB;(2)、类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=2,将斜边AB绕点A逆时针旋转90°至AB',连接B′C,求△AB′C的面积.(3)、拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上且OC=2cm,动点P从点E沿射线EC以lcm/s速度运动,连接OP,将线段OP绕点O逆时针旋转120°得到线段OF,设点P运动的时间为t秒.①当t=秒时,OF∥ED.
②当t=秒时,点F恰好落在射线EB上.
