河南省安阳市汤阴县2019-2020学年八年级上学期数学期中s考试试卷
试卷更新日期:2020-10-09 类型:期中考试
一、选择题
-
1. 在以下四个图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组线段为边,能组成三角形的是( )
2. 以下列各组线段为边,能组成三角形的是( )
A、1cm,2cm,4cm B、4cm,6cm,8cm C、5cm,6cm,12cm D、2cm,3cm,5cm3. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则∠1+∠2等于( ) A、60° B、75° C、90° D、105°4. 如果两个三角形全等,则不正确的是( )A、它们的最小角相等 B、它们的对应外角相等 C、它们是直角三角形 D、它们的最长边相等5. 等腰三角形的一个角是 ,则它的底角是( )A、 B、 C、 或 D、 或6. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
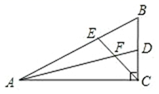
A、60° B、75° C、90° D、105°4. 如果两个三角形全等,则不正确的是( )A、它们的最小角相等 B、它们的对应外角相等 C、它们是直角三角形 D、它们的最长边相等5. 等腰三角形的一个角是 ,则它的底角是( )A、 B、 C、 或 D、 或6. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( ) A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF7. 如图所示,等腰 中, , 平分 ,交 于 ,过 作 于 ,若 , ,那么 的长度是( )
A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF7. 如图所示,等腰 中, , 平分 ,交 于 ,过 作 于 ,若 , ,那么 的长度是( ) A、a+b B、 C、a+2b D、8. 如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )
A、a+b B、 C、a+2b D、8. 如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( ) A、1 B、2 C、3 D、49. 如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( )
A、1 B、2 C、3 D、49. 如图是一个经过改造的规则为3×5的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过台球边缘多次反弹),那么球最后将落入的球袋是( ) A、1号袋 B、2号袋 C、3号袋 D、4号袋10. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( )
A、1号袋 B、2号袋 C、3号袋 D、4号袋10. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=42°,则∠P的度数为( ) A、44° B、66° C、96° D、92°
A、44° B、66° C、96° D、92°二、填空题
-
11. 点M(2,-3)关于y轴对称的对称点N的坐标是.12. 如果一个正多边形的每个外角是60°,则这个正多边形的对角线共有条.13. 如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm.求△ABC的周长.
 14. 当三角形中一个内角 是另一个内角 的两倍时,我们称此三角形为“特征三角形”,其中 称为“特征角”如果一个“特征三角形”的“特征角”为 时,那么这个“特征三角形”的最小内角度数是.15. 如下图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是.
14. 当三角形中一个内角 是另一个内角 的两倍时,我们称此三角形为“特征三角形”,其中 称为“特征角”如果一个“特征三角形”的“特征角”为 时,那么这个“特征三角形”的最小内角度数是.15. 如下图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是.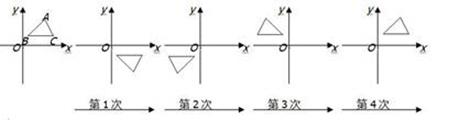
三、解答题
-
16. 已知:如图,AB∥CD,BF=DE,点B、E、F、D在同一直线上,∠A=∠C求证:AE=CF.
 17. 如图,在 的正方形网格中, 是格点三角形,点 的坐标分别为 , .
17. 如图,在 的正方形网格中, 是格点三角形,点 的坐标分别为 , . (1)、①在图中画出相应的平面直角坐标系;
(1)、①在图中画出相应的平面直角坐标系;②画出 关于直线 对称的 ,并标出点 的坐标;
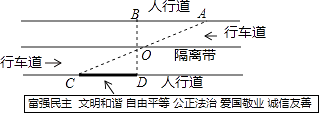
(2)、若点 在 内,其关于直线 的对称点是 ,则 的坐标是.18. 如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N. (1)、求证:△AMC≌△CNB;(2)、求证:MN=AM+BN.19. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:
(1)、求证:△AMC≌△CNB;(2)、求证:MN=AM+BN.19. 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.
 20. 如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE.
20. 如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC的中点,AE与BD相交于点F,连接DE. (1)、求证:△ABE≌△BCD;(2)、判断线段AE与BD的数量关系及位置关系,并说明理由;21. 如图①所示,在三角形纸片 中, , ,将纸片的一角折叠,使点 落在 内的点 处.
(1)、求证:△ABE≌△BCD;(2)、判断线段AE与BD的数量关系及位置关系,并说明理由;21. 如图①所示,在三角形纸片 中, , ,将纸片的一角折叠,使点 落在 内的点 处.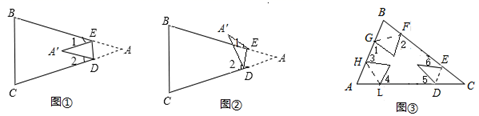 (1)、若 , .(2)、如图①,若各个角度不确定,试猜想 , , 之间的数量关系,直接写出结论.
(1)、若 , .(2)、如图①,若各个角度不确定,试猜想 , , 之间的数量关系,直接写出结论.②当点 落在四边形 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立, , , 之间又存在什么关系?请说明.
(3)、应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的 和是.