陕西省咸阳市武功县2019-2020学年高一上学期数学期中考试试卷

试卷更新日期：2020-10-09 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {y | y = 3^{1 - x} ， x \in R} ， B = {x | 1 \leq x \leq 4}$ ，则（）

A、 $A \cup B = (0 ， + \infty)$ B、 $A \cap B = [1 ， 3]$ C、 $A \cap B = ϕ$ D、 $A \cap B = (0 ， 4]$

查看试题解析
2. 函数 $y = \frac{\sqrt{x}}{\lg (2 - x)}$ 的定义域是（）

A、[0，2) B、[0，1)∪(1，2) C、(1，2) D、[0，1)

查看试题解析
3. 下列各组函数，在同一直角坐标系中， $f (x)$ 与 $g (x)$ 有相同图像的一组是（）

A、 $f (x) = {(x^{2})}^{\frac{1}{2}}$ ， $g (x) = {(x^{\frac{1}{2}})}^{2}$ B、 $f (x) = \frac{x^{2} - 9}{x + 3}$ ， $g (x) = x - 3$ C、 $f (x) = {(x^{\frac{1}{2}})}^{2}$ ， $g (x) = 2 \log_{2} x$ D、 $f (x) = x$ ， $g (x) = \lg 10^{x}$

查看试题解析
4. 已知幂函数f（x）=（m﹣3）x^m ，则下列关于f（x）的说法不正确的是（　　）

A、f（x）的图象过原点 B、f（x）的图象关于原点对称 C、f（x）的图象关于y轴对称 D、f（x）=x⁴

查看试题解析
5. 已知函数f(x)在区间[a，b]上单调，且图象是连续不断的，若f(a)·f(b)＜0，则方程f(x)＝0在区间[a，b]上（）

A、至少有一实数根 B、至多有一实数根 C、没有实数根 D、必有唯一的实数根

查看试题解析
6. 下列各式中成立的是（）

A、 ${(\frac{m}{n})}^{7} = n^{7} m^{\frac{1}{7}}$ B、 $\sqrt[12]{{(- 3)}^{4}} = \sqrt[3]{- 3}$ C、 $\sqrt[4]{x^{3} + y^{3}} = {(x + y)}^{\frac{3}{4}}$ D、 $\sqrt{\sqrt[3]{9}} = \sqrt[3]{3}$

查看试题解析
7. 设函数 $f (x) = {\begin{array}{l} 2 e^{x - 1}, x < 2 \\ \log_{3} (x^{2} - 1), x \geq 2 \end{array}$ ，则 $f (f (2))$ 的值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 设a=e^0.3 ， b=0.9² ， c=ln0.9，则a，b，c的大小关系是（　　）

A、a＜b＜c B、c＜b＜a C、c＜a＜b D、b＜c＜a

查看试题解析
9. 如果 ${log}_{a} 3 > {log}_{b} 3 > 0$ ，那么 $a, b$ 间的关系是（）

A、 $0 < a < b < 1$ B、 $1 < a < b$ C、 $0 < b < a < 1$ D、 $1 < b < a$

查看试题解析
10. 已知函数：① $y = 2^{x}$ ；② $y = \log_{2} x$ ；③ $y = x^{- 1}$ ；④ $y = x^{\frac{1}{2}}$ ，则下列函数图象（第一象限部分）从左到右依次与函数序号的对应顺序是（）

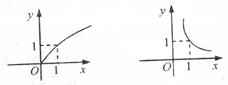A、①②④③ B、②③①④ C、②①③④ D、④①③②

查看试题解析

11. 根据表格中的数据，可以判定函数

f (x) = e^{x} - x - 2

的一个零点所在的区间为（）

$x$	-1	0	1	2	3
$e^{x}$	0.37	1	2.72	7.39	20.09
$x + 2$	1	2	3	4	5

A、

(- 1, 0)

B、

(0, 1)

C、

(2, 3)

D、

(1, 2)

查看试题解析

12. 当 $x \in (1, 2)$ 时，不等式 ${(x - 1)}^{2} < \log_{a} x$ 恒成立，则 $a$ 的取值范围是（）

A、 $(0, 1)$ B、 $(1, 2)$ C、 $(1, 2]$ D、 $(0, \frac{1}{2})$

查看试题解析

二、填空题

13. 函数 $y = a^{x - 5} + 6$ 的图象恒过定点.

查看试题解析
14. 已知 $x {log}_{2} 3 = 1$ ，则 $3^{x} =$ ．

查看试题解析
15. 下列说法中，正确的是(填序号)．
①任取x＞0，均有3^x＞2^x；

②当a＞0，且a≠1时，有a³＞a²；

③y＝( $\sqrt{3}$ )^－^x是增函数；

④y＝2^|x|的最小值为1；

⑤在同一坐标系中，y＝2^x与y＝2^－^x的图象关于y轴对称．

查看试题解析
16. 某厂2006年的产值为 $a$ 万元，预计产值每年以 $n %$ 递增，则该厂到2019年末的产值（单位：万元）是.

查看试题解析

三、解答题

17. 计算：

(1)、 ${(2 \frac{7}{9})}^{0.5} + {0.1}^{- 2} + {(2 \frac{10}{27})}^{- \frac{2}{3}} - 3 π^{0} + \frac{37}{3} \times 2^{- 4}$ ；

(2)、 $\log_{2.5} 6.25 + \lg 0.01 + \ln \sqrt{e} + 2^{1 + \log_{2} 3}$ .

查看试题解析
18. 求函数 $f (x) = - {(\log_{\frac{1}{2}} x)}^{2} - \log_{\frac{1}{4}} x + 5$ 在区间 $[2, 4]$ 内的最值.

查看试题解析
19. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，当 $x \geq 0$ 时， $f (x) = a^{x} - 1$ 其中 $a > 0$ 且 $a \neq 1$ .

(1)、求 $f (2) + f (- 2)$ 的值；

(2)、求 $x < 0$ 时， $f (x)$ 的解析式.

查看试题解析
20. 函数 $f (x) = \log_{2} | x | + 1$ .

(1)、用定义证明 $f (x)$ 是偶函数；

(2)、解不等式： $f (x) \geq 3$ .

查看试题解析
21. 已知函数 $f (x) = m - \frac{2}{2^{x} + 1}$ 是 $R$ 上的奇函数.

(1)、求 $m$ 的值；

(2)、先判断 $f (x)$ 的单调性，再证明之.

查看试题解析
22. 已知一次函数 $f (x)$ 满足： $f (1) = 2, f (2) = 3$ .

(1)、求 $f (x)$ 的解析式；

(2)、判断函数 $g (x) = - 1 + \lg f^{2} (x)$ 在区间 $[0, 9]$ 上零点的个数.

查看试题解析