高中数学人教新课标A版选修2-2 1.3导数在研究函数中的应用

试卷更新日期：2020-10-06 类型：同步测试

进入出卷网下载

一、单选题

1. 函数 $f (x) = x^{4} - 2 x^{3}$ 的图像在点 $(1 ， f (1))$ 处的切线方程为（）

A、 $y = - 2 x - 1$ B、 $y = - 2 x + 1$ C、 $y = 2 x - 3$ D、 $y = 2 x + 1$

查看试题解析
2. 函数 $f (x) = (x + 2) e^{x}$ 的单调递增区间是（）

A、 $(- \infty ， 3)$ B、 $(0 ， 3)$ C、 $(- 3 ， 0)$ D、 $(- 3 ， + \infty)$

查看试题解析
3. 若曲线 $y = f (x) = x^{2} + a x + b$ 在点 $(0 ， b)$ 处的切线方程是 $x - y + 1 = 0$ ，则（）

A、 $a = 1 ， b = 1$ B、 $a = - 1 ， b = 1$ C、 $a = 1 ， b = - 1$ D、 $a = - 1 ， b = - 1$

查看试题解析
4. 曲线 $f (x) = x^{3} - x$ 在点 $(- 1 ， f (- 1))$ 处的切线方程为（）

A、 $2 x + y + 2 = 0$ B、 $2 x + y - 2 = 0$ C、 $2 x - y + 2 = 0$ D、 $2 x - y - 2 = 0$

查看试题解析
5. 已知函数 $f (x)$ 在 $x_{0}$ 处的导数为 $f^{'} (x_{0})$ ，则 $\lim_{Δ x \to 0} \frac{f (x_{0}) - f (x_{0} - m Δ x)}{Δ x}$ 等于（）

A、 $m f^{'} (x_{0})$ B、 $- m f^{'} (x_{0})$ C、 $- \frac{1}{m} f^{'} (x_{0})$ D、 $\frac{1}{m} f^{'} (x_{0})$

查看试题解析
6. 已知函数 $f (x) = \sqrt{x}$ 在点 $x = x_{0}$ 处的切线的倾斜角是 $\frac{π}{4}$ ，则 $x_{0}$ 的值为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、1

查看试题解析
7. 已知函数 $f (x)$ 在 $x > 0$ 上可导且满足 $x f^{'} (x) - f (x) > 0$ ，则下列一定成立的为（）

A、 $e f (π) > π f (e)$ B、 $f (π) < f (e)$ C、 $\frac{f (π)}{π} < \frac{f (e)}{e}$ D、 $f (π) > f (e)$

查看试题解析
8. 若点P是曲线 $y = x^{2} - \ln x$ 上任一点，则点P到直线 $x - y - 4 = 0$ 的最小距离是（）

A、 $\sqrt{2}$ B、3 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
9. 若函数 $f (x) = \frac{1}{2} x^{2} - 9 \ln x$ 在区间 $[a - 1 ， a]$ 上单调递减，则实数a的取值范围是（）

A、 $1 < a \leq 3$ B、 $a \geq 4$ C、 $a \leq 3$ D、 $1 < a \leq 4$

查看试题解析
10. 已知定义域为R的奇函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，当 $x > 0$ 时， $x f^{'} (x) > f (x)$ .若 $a = \frac{f (- \log_{2} 3)}{- \log_{2} 3} ， b = \frac{f (\log_{4} 6)}{\log_{4} 6} ， c = \frac{f (\sin \frac{π}{8})}{\sin \frac{π}{8}}$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $a < b < c$ B、 $c < a < b$ C、 $c < b < a$ D、 $b < c < a$

查看试题解析
11. 已知 $f (x)$ 在R上是可导函数，则 $f (x)$ 的图象如图所示，则不等式 $(x^{2} - 2 x - 3) f^{'} (x) > 0$ 的解集为（）

A、 $(- \infty ， - 2) \cup (1 ， + \infty)$ B、 $(- \infty ， - 2) \cup (1 ， 2)$ C、 $(- \infty ， - 1) \cup (- 1 ， 0) \cup (2 ， + \infty)$ D、 $(- \infty ， - 1) \cup (- 1 ， 1) \cup (3 ， + \infty)$

查看试题解析
12. 已知定义在R上的函数 $f (x)$ 满足 $f (1) = 1$ ，且 $f' (x) > \frac{1}{2}$ 恒成立，则不等式 $f (x^{2}) < \frac{x^{2}}{2} + \frac{1}{2}$ 的解集为（）

A、 $(- \infty ， - 1)$ B、 $(1 ， + \infty)$ C、 $(- \infty ， - 1) \cup (1 ， + \infty)$ D、 $(- 1 ， 1)$

查看试题解析
13. 设 $f (x)$ 是在 $(0 ， + \infty)$ 上的可导函数，且 $f^{'} (x) \geq \frac{2}{x} f (x)$ ， $f (1) = 4$ ， $f (2) = 16$ ，则下列一定不成立的是（）

A、 $f (\frac{3}{2}) = 8$ B、 $f (3) = 40$ C、 $f (4) = 72$ D、 $f (5) = 120$

查看试题解析
14. 已知 $f (x) = \frac{e^{x}}{x} - 2 t (\ln x + x + \frac{2}{x})$ 恰有一个极值点为1，则t的取值范围是（）

A、 $(- \infty ， \frac{1}{4}] \cup {\frac{e}{6}}$ B、 $f (x) = {\begin{cases} 2^{x} ， \begin{matrix} \end{matrix} x \leq 0 ， \\ - x^{2} + 1 ， x > 0 \end{cases}$ C、 $[0 ， \frac{1}{4}] \cup {\frac{e}{6}}$ D、 $(- \infty ， \frac{1}{4}]$

查看试题解析

二、多选题

15. 已知函数 $y = f (x)$ 的导函数的图象如图所示，下列结论中正确的是（）

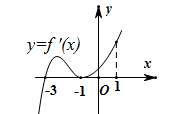A、-1是函数 $f (x)$ 的极小值点 B、-3是函数 $f (x)$ 的极小值点 C、函数 $f (x)$ 在区间 $(- 3 ， 1)$ 上单调递增 D、函数 $f (x)$ 在 $x = 0$ 处切线的斜率小于零

查看试题解析
16. 已知函数 $f (x) = x \ln x$ ，若 $0 < x_{1} < x_{2}$ ，则下列选项正确的是（）

A、 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ B、 $x_{1} + f (x_{1}) < x_{2} + f (x_{2})$ C、 $x_{2} f (x_{1}) < x_{1} f (x_{2})$ D、当 $x_{2} > x_{1} > \frac{1}{e}$ 时， $x_{1} f (x_{1}) + x_{2} f (x_{2}) > x_{2} f (x_{1}) + x_{1} f (x_{2})$

查看试题解析

三、填空题

17. 若曲线 $y = a x^{2} - \ln x$ 在点 $(1, a)$ 处的切线平行于x轴，则a= ．

查看试题解析
18. 函数 $f (x) = x^{3} + a x$ （ $x \in R$ ）在 $x = 1$ 处有极值，则曲线 $y = f (x)$ 在原点处的切线方程是．

查看试题解析
19. 曲线 $y = \ln x + x + 1$ 的一条切线的斜率为2，则该切线的方程为.

查看试题解析
20. 已知函数 $f (x) = (x e^{x} - m) x - 2 e^{x} (x \in R)$ .
若 $m = 0$ ，则 $f (x)$ 的极大值点为．

若 $f (x)$ 有3个极值点，则实数m的取值范围是．

查看试题解析
21. 已知函数 $f (x) = {\begin{array}{l} e^{2 x} (x > 0) \\ x^{2} + 4 (x \leq 0) \end{array}$ ，若 $\forall x \in R$ ， $f (x) \geq m x$ ，则实数m的取值范围是．

查看试题解析
22. 已知 $f (x) = x (e + \ln x)$ ， $g (x) = \frac{1}{3} x^{3} + \frac{3}{2} x + m$ ，对于 $\forall x \in [\frac{1}{2} ， + \infty)$ 时都有 $f (x) \leq g (x)$ 恒成立，则m的取值范围为.

查看试题解析

四、解答题

23. 设函数 $f (x) = - \ln x + m x^{2} - 2 x$ (m $\in$ R).

(1)、当 $m = 1$ 时，求函数 $f (x)$ 在 $x = 1$ 处的切线方程；

(2)、当 $m = \frac{3}{2}$ 时，求函数 $f (x)$ 的单调增区间.

查看试题解析
24. 已知函数 $f (x) = a x^{3} + x^{2} (a \in R)$ 在 $x = - \frac{4}{3}$ 处取得极值.

(1)、求实数a的值；

(2)、若 $g (x) = f (x) \cdot e^{x}$ （其中e为自然对数的底数），求曲线 $g (x)$ 在点 $(1 ， g (1))$ 处的切线的方程.

查看试题解析
25. 已知函数 $f (x) = (x + 1) \cdot (\ln (x + 1) - 1)$ .

(1)、求函数 $f (x)$ 的单调区间和极值；

(2)、若函数 $g (x) = f (x) - a x - b (a ， b \in R)$ 在区间 $[0 ， 1]$ 上存在零点，求 $a^{2} + b$ 的最小值.（参考数据： $\ln 2 \approx 0.6931$ ）

查看试题解析
26. 已知函数 $f (x) = \ln x + \frac{2 a}{x} ， a \in R$ .

(1)、若函数 $f (x)$ 在 $[4 ， + \infty)$ 上是增函数，求实数a的取值范围；

(2)、若函数 $f (x)$ 在 $[1 ， e]$ 上的最小值为3，求实数a的值.

查看试题解析
27. 设 $f (x) = e^{x} \sin x$ 函数.
(Ⅰ)求函数 $f (x)$ 单调递增区间；

(Ⅱ)当 $x \in [0 ， π]$ 时，求函数 $f (x)$ 的最大值和最小值.

查看试题解析
28. 已知函数f（x）=2lnx+1．

(1)、若f（x）≤2x+c，求c的取值范围；

(2)、设a>0时，讨论函数g（x）= $\frac{f (x) - f (a)}{x - a}$ 的单调性．

查看试题解析
29. 已知函数 $f (x) = e^{x} + a x^{2} - x$ .

(1)、当a=1时，讨论f（x）的单调性；

(2)、当x≥0时，f（x）≥ $\frac{1}{2}$ x³+1，求a的取值范围.

查看试题解析
30. 已知函数 $f (x) = a e^{x - 1} - \ln x + \ln a$ ．

(1)、当 $a = e$ 时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

(2)、若f（x）≥1，求a的取值范围．

查看试题解析

高中数学人教新课标A版 选修2-2 1.3导数在研究函数中的应用

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教新课标A版选修2-2 1.3导数在研究函数中的应用