云南省临沧市2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-26 类型：期末考试

进入出卷网下载

一、填空题

1. 比较大小：﹣π﹣3.14（选填“＞”、“=”、“＜”）．

查看试题解析
2. 若甲看乙的方向为南偏西25°，则乙看甲的方向是．

查看试题解析
3. 若 $\frac{3}{2}$ x^by⁴与﹣5x³y^4a是同类项，则a﹣b= ．

查看试题解析
4.
如图，小聪把一块含有30°角的直角三角尺ABC的两个顶点A，C放在长方形纸片DEFG的对边上，若AC平分∠BAE，则∠DAB的度数是．

查看试题解析
5. 关于x的方程4（a﹣1）=3a+x﹣9的解为非负数，则a的取值范围是．

查看试题解析
6. 一个角的补角比它的余角的3倍还多10°，则这个角的度数为．

查看试题解析

二、选择题

7. ﹣2017的倒数是（）

A、2017 B、﹣2017 C、 $\frac{1}{2017}$ D、﹣ $\frac{1}{2017}$

查看试题解析
8. 下列命题中的假命题是（）

A、同位角一定相等 B、平移不改变图形的形状和大小 C、无理数是无限不循环小数 D、点M（a，﹣a）可能在第二象限

查看试题解析
9. 长城总长约为6700000米，用科学记数法表示为（）

A、67×10⁵米 B、6.7×10⁶米 C、6.7×10⁷米 D、6.7×10⁸米

查看试题解析
10.
如图，已知直线a∥b，∠1=70°，那么∠2的度数是（）

A、60° B、80° C、90° D、110°

查看试题解析
11.
小强制作了一个正方体模型的展开图，如图所示，把“读书使人进步”六个字分别粘贴在六个面上，那么在正方体模型中与“书”相对的面上的字是（）

A、使 B、人 C、进 D、步

查看试题解析
12. 式子 $\sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、x＞1 B、x＜1 C、x≥1 D、x≤1

查看试题解析
13. 已知整式x²﹣2x的值为6，则代数式5﹣2x²+4x的值为（）

A、8 B、﹣7 C、11 D、﹣17

查看试题解析
14.
如图是按一定规律摆放的图案，按此规律，下列图案中与第2017个图案中的指针指向相同的图案是（）

A、第1个 B、第2个 C、第3个 D、第4个

查看试题解析

三、解答题

15. 计算：

(1)、（﹣2）³﹣[4÷（﹣ $\frac{2}{3}$ ）²+1]+（﹣1）²⁰¹⁷

(2)、（﹣1）²+ $\sqrt[3]{27}$ +|﹣3|× $\sqrt{2}$ ．

查看试题解析
16.
解不等式组 ${\begin{matrix} 2 x + 1 < - 1 \\ 3 - x \geq 1 \end{matrix}$ ，并将解集在数轴上表示出来．

查看试题解析
17. 先化简，再求值：x﹣3（x﹣ $\frac{1}{3}$ y²）+6（﹣x+ $\frac{1}{3}$ y²），其中x=﹣2，y= $\sqrt{2}$ ．

查看试题解析
18.
为了了解光明中学学生平均每周的体育锻炼时间，小敏在校内随机调查了50名同学，统计并绘制了频数分布表（如下表）和扇形统计图（如图）．
组别
锻炼时间（h/周）
频数
A
1.5≤t＜3
1
B
3≤t＜4.5
2
C
4.5≤t＜6
a
D
6≤t＜7.5
20
E
7.5≤t＜9
15
F
t≥9
b

(1)、a= ， b= ．

(2)、在扇形统计图中，D组所占圆心角的度数为．

(3)、全校共有3000名学生，请你帮助小敏估计该校平均每周体育锻炼时间不少于6h的学生约有多少人？

查看试题解析
19.
如图，EG⊥BC于点G，AD⊥BC于点D，∠1=∠E，请证明AD平分∠BAC．

查看试题解析
20.
如图所示，在平面直角坐标系中，已知A、B、C三点的坐标分别为A（﹣1，5），B（﹣3，0），C（﹣4，3）．

(1)、画出把△ABC向右平移6个单位，再向上平移1个单位长度的三角形A′B′C′；

(2)、写出平移后三角形A′B′C′的各顶点的坐标；

(3)、求三角形A′B′C′的面积．

查看试题解析
21.
如图所示，线段AB=6cm，点C是线段AB上任意一点，点M是线段AC的中点，点N是线段BC的中点，求线段MN的长．

查看试题解析
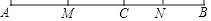22. 把文字翻译成数学符号，构建方程组模型是解此类题的关键；方案型问题就是要构建双边不等式，有几个整数解就有几种方案；某工程队现有大量的沙石需要运输．工程队下属车队有载重量为8吨、10吨的卡车共12辆，全部车辆运输一次能运输110吨沙石．

(1)、求该车队载重量为8吨、10吨的卡车各有多少辆？

(2)、随着工程的进展，车队需要一次运输沙石165吨以上，为了完成任务，准备新增购这两种卡车共6辆，车队有多少种购买方案，请你一一写出．

查看试题解析
23.
如图所示，数轴上有A、B、C、D四个点，分别对应的数为a、b、c、d，且满足a=﹣2，|b|=0，（c﹣12）²与|d﹣18|互为相反数．

(1)、b=；c=；d= ．

(2)、若A、B两点以2个单位长度/秒的速度向右匀速运动，同时C、D两点以1个单位长度/秒的速度向左匀速运动，并设运动时间为t秒，问t为多少时，A、C两点相遇？

(3)、在（2）的条件下，A、B、C、D四点继续运动，当点B运动到点D的右侧时，问是否存在时间t，使得B与D的距离是C与D的距离的3倍？若存在，求时间t；若不存在，请说明理由．

查看试题解析

组别	锻炼时间（h/周）	频数
A	1.5≤t＜3	1
B	3≤t＜4.5	2
C	4.5≤t＜6	a
D	6≤t＜7.5	20
E	7.5≤t＜9	15
F	t≥9	b