山西省晋中市农大附中2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2017-09-26 类型:期末考试
一、选择题
-
1. 下列各式不能成立的是( )A、(x2)3=x6 B、x2•x3=x5 C、(x﹣y)2=(x+y)2﹣4xy D、x2÷(﹣x)2=﹣12. 给出下列图形名称:(1)线段;(2)直角;(3)等腰三角形;(4)平行四边形;(5)长方形,在这五种图形中是轴对称图形的有( )A、1个 B、2个 C、3个 D、4个3. 在下列多项式的乘法中,可用平方差公式计算的是( )A、(2+a)(a+2) B、( a+b)(b﹣ a) C、(﹣x+y)(y﹣x) D、(x2+y)(x﹣y2)4. 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1 , 在乙种地板上最终停留在黑色区域的概率为P2 , 则( )
 A、P1>P2 B、P1<P2 C、P1=P2 D、以上都有可能5. 在同一平面内,如果两条直线被第三条直线所截,那么( )A、同位角相等 B、内错角相等 C、不能确定三种角的关系 D、同旁内角互补6. 如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )
A、P1>P2 B、P1<P2 C、P1=P2 D、以上都有可能5. 在同一平面内,如果两条直线被第三条直线所截,那么( )A、同位角相等 B、内错角相等 C、不能确定三种角的关系 D、同旁内角互补6. 如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )( 1 )汽车行驶时间为40分钟;
( 2 )AB表示汽车匀速行驶;
( 3 )在第30分钟时,汽车的速度是90千米/时;
( 4 )第40分钟时,汽车停下来了.
 A、1个 B、2个 C、3个 D、4个7. 如图,AB∥ED,则∠A+∠C+∠D=( )
A、1个 B、2个 C、3个 D、4个7. 如图,AB∥ED,则∠A+∠C+∠D=( ) A、180° B、270° C、360° D、540°8. 已知一个正方体的棱长为2×102毫米,则这个正方体的体积为( )A、6×106立方毫米 B、8×106立方毫米 C、2×106立方毫米 D、8×105立方毫米9. 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
A、180° B、270° C、360° D、540°8. 已知一个正方体的棱长为2×102毫米,则这个正方体的体积为( )A、6×106立方毫米 B、8×106立方毫米 C、2×106立方毫米 D、8×105立方毫米9. 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,
四个结论中成立的是( )
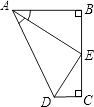 A、①②④ B、①②③ C、②③④ D、①③10.
A、①②④ B、①②③ C、②③④ D、①③10.如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )
 A、
A、 B、
B、 C、
C、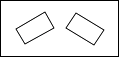 D、
D、
二、填空题
-
11. 任意翻一下2016年的日历,翻出1月6日是事件,翻出4月31日是事件.(填“确定”或“不确定”)12. 等腰三角形一边长为8,另一边长为5,则此三角形的周长为.13. 若x2+6x+b2是一个完全平方式,则b的值是 .14. 在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有(填序号)15. 如图,已知C,D两点在线段AB上,AB=10cm,CD=6cm,M,N分别是线段AC,BD的中点,则MN=cm.
 16. 一辆小车由静止开始从光滑的斜面上向下滑动,通过观察记录小车滑动的距离s(m)与时间t(s)的数据如下表:
16. 一辆小车由静止开始从光滑的斜面上向下滑动,通过观察记录小车滑动的距离s(m)与时间t(s)的数据如下表:时间t(s)
1
2
3
4
距离s(m)
2
8
18
32
…
则写出用t表示s的关系式s= .
三、解答题
-
17. 计算:
(1)、简便计算:(2)、计算:2a3b2•(﹣3bc2)3÷(﹣ca2)(3)、先化简再求值:[(3x+2y)(3x﹣2y)﹣(x+2y)(5x﹣2y)]÷4x,其中x= ,y=2.18.“西气东输”是造福子孙后代的创世纪工程.现有两条高速公路和A、B两个城镇(如图),准备建立一个燃气中心站P,使中心站到两条公路距离相等,并且到两个城镇距离相等,请你画出中心站位置.
 19. 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.
19. 如图所示,转盘被等分成六个扇形,并在上面依次写上数字1、2、3、4、5、6.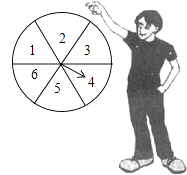 (1)、若自由转动转盘,当它停止转动时,指针指向奇数区的概率是多少?(2)、请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为 .20.
(1)、若自由转动转盘,当它停止转动时,指针指向奇数区的概率是多少?(2)、请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为 .20.如图,已知∠1=∠2,∠3=∠4,∠E=90°,试问:AB∥CD吗?为什么?

解:∵∠1+∠3+∠E=180°∠E=90°
∴∠1+∠3=
∵∠1=∠2,∠3=∠4
∴∠1+∠2+∠3+∠4=
∴AB∥CD .
21. 星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.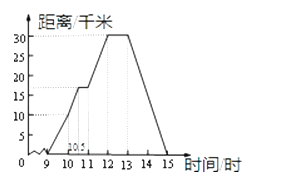 (1)、玲玲到达离家最远的地方是什么时间?离家多远?(2)、她何时开始第一次休息?休息了多长时间?(3)、她骑车速度最快是在什么时候?车速多少?(4)、玲玲全程骑车的平均速度是多少?22.
(1)、玲玲到达离家最远的地方是什么时间?离家多远?(2)、她何时开始第一次休息?休息了多长时间?(3)、她骑车速度最快是在什么时候?车速多少?(4)、玲玲全程骑车的平均速度是多少?22.把两个含有45°角的直角三角板如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
 23. 暑假期间某中学校长决定带领市级“三好学生”去北京旅游,甲旅行社承诺:“如果校长买全票一张,则学生可享受半价优惠”;乙旅行社承诺:“包括校长在内所有人按全票的6折优惠”.若全票价为240元(1)、设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别写出两个旅行社收费的表达式.(2)、当学生人数为多少时,两旅行社收费相同?24. 如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
23. 暑假期间某中学校长决定带领市级“三好学生”去北京旅游,甲旅行社承诺:“如果校长买全票一张,则学生可享受半价优惠”;乙旅行社承诺:“包括校长在内所有人按全票的6折优惠”.若全票价为240元(1)、设学生数为x,甲、乙旅行社收费分别为y甲(元)和y乙(元),分别写出两个旅行社收费的表达式.(2)、当学生人数为多少时,两旅行社收费相同?24. 如图1,线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P. (1)、找出图中的所有全等三角形.(2)、找出一组相等的线段,并说明理由.(3)、如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.
(1)、找出图中的所有全等三角形.(2)、找出一组相等的线段,并说明理由.(3)、如图2,取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.