江西省萍乡市2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-26 类型：期末考试

进入 出卷网 下载

一、选择题

  • 1. 下面所给的交通标志图中是轴对称图形的是

    A、 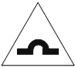B、 C、 D、

    查看试题解析

  • 2. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物，将0.0000025用科学记数法表示为（   ）
    A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣6

    查看试题解析

  • 3. 如图，直线a，b被c所截，a∥b，若∠1=35°，则∠2的大小为（   ）


    A、35° B、145° C、55° D、125°

    查看试题解析

  • 4. 下列运算，计算结果正确的是（   ）
    A、a4•a3=a12 B、a6÷a3=a2 C、（a3）2=a5 D、a3•b3=（a•b）3

    查看试题解析

  • 5. 小米和小亮玩一种跳棋游戏，如图，游戏板由大小相等的小正方形组成，小米让棋子在游戏板上随意走动，则棋子落在白色区域的概率是（   ）

    A、13 B、38 C、58 D、916

    查看试题解析

  • 6. 如图，OA，BA分别表示甲、乙两名学生运动路程与时间的关系图象，图中s和t分别表示运动路程和时间，根据图象判定快者的速度比慢者的速度每秒快（   ）

    A、1m B、1.5m C、2m D、2.5m

    查看试题解析

  • 7. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，请你根据所学的图形的全等这一章的知识，说明画出∠A′O′B′=∠AOB的依据是（   ）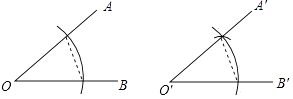

    A、SAS B、ASA C、AAS D、SSS

    查看试题解析

  • 8. 如图，在△ABC中，AB=AC，AB+BC=8，将△ABC折叠，使点A落在点B处，折痕为DF，则△BCF的周长是（   ）

    A、8 B、16 C、4 D、10

    查看试题解析

  • 9. 请你计算：（1﹣x）（1+x），（1﹣x）（1+x+x2），…，猜想（1﹣x）（1+x+x2+…+xn）的结果是（   ）
    A、1﹣xn+1 B、1+xn+1 C、1﹣xn D、1+xn

    查看试题解析

  • 10. △ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过点C作CF⊥AE，垂足为点F，过点B作BD⊥BC交CF的延长线于点D，BD=2cm，则△ABE的面积为（   ）


    A、2cm2 B、4cm2 C、6cm2 D、8cm2

    查看试题解析

二、填空题

  • 11. 计算： 9xy⋅(−13x2y) = ．

    查看试题解析

  • 12. 某十字路口有一交通信号灯，红灯亮25秒，绿灯亮20秒，黄灯亮5秒，当你抬头看信号灯时，恰好是黄灯的概率是 ．

    查看试题解析

  • 13. 如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线MN交AC于点D，则∠DBC=°．

    查看试题解析

  • 14. 若a的值使得x2+4x+a=（x+2）2﹣1成立，则a的值为 ．

    查看试题解析

  • 15. 李冰买了一张30元的租碟卡，每租一张碟后卡中剩余金额y（元）与租碟张数x（张）之间的关系式为

    租碟数/张

    卡中余额/元

    1

    30﹣0.8

    2

    30﹣1.6

    3

    30﹣2.4

    …

    …

    查看试题解析

  • 16. 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF=AC，则∠ABC=度．

    查看试题解析

  • 17. 如图，在∠AOB的内部有一点P，点M、N分别是点P关于OA，OB的对称点，MN分别交OA，OB于C，D点，若△PCD的周长为30cm，则线段MN的长为cm．

    查看试题解析

  • 18. 如图：在△ABC中，AB=AC，BC=BD，AD=DE=EB，则∠A= ．

    查看试题解析

三、解答题

  • 19. 计算下列各式：
    (1)、（﹣2）0+（ 12 ）﹣2﹣（﹣0.5）2016•22017
    (2)、先化简，再求值：（a+b）（a﹣b）+（a+b）2﹣2a2 ， 其中a=2017，b=﹣ 12017 ．

    查看试题解析

  • 20. 如图所示，点O为直线BD上的一点，OC⊥OA，垂足为点O，∠COD=2∠BOC，求∠AOB的度数．

    查看试题解析

  • 21. 如图，∠1：∠2：∠3=2：3：4，∠AFE=60°，∠BDE=120°，写出图中平行的直线，并说明理由．

    查看试题解析

四、解答题

  • 22. 口袋里有红、绿、黄三种颜色的球，除颜色外其余均相同，其中有红球4个，绿球3个，任意摸出一个球是绿球的概率是 16 ．试求：
    (1)、口袋里黄球的个数；
    (2)、任意摸出一个球是黄球的概率．

    查看试题解析

  • 23. “三月三，放风筝”如图是小颖制作的风筝，他根据AD=BD，AC=BC，不用度量，就知道∠DAC=∠DBC，请你运用所学的知识，给予说明．

    查看试题解析

五、解答题

  • 24. 如图，AD为△ABC的角平分线，DE⊥AC于E，DF⊥AB于F，EF交AD于点M．

    (1)、试说明：MF=ME；
    (2)、若△ABC的面积为28cm2 ， AB=20cm，AC=8cm，求DE的长．

    查看试题解析

  • 25. 如图所示，A，B两地相距50千米，甲于某日下午1时骑自行车从A地出发驶往B地，乙也于同日下午2时骑摩托车按同路从A地出发驶往B地，图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午行驶的时间t之间的关系．根据图象回答下列问题：

    (1)、甲在该日下午2﹣5时骑自行车的速度是多少？
    (2)、乙从出发大约用多长时间就能追上甲？
    (3)、甲骑自行车和乙骑摩托车在全程的平均速度分别是多少？

    查看试题解析

六、解答题

  • 26. 问题背景：如图（1），在△ABC中，已知AB=AC，BE=CF．

    (1)、发现问题：小华审题后发现，若连接CE，BF，则CE=BF，请说明理由；
    (2)、提出问题：如图（2），设CE与BF交于点O，则直线AO是BC边的垂直平分线吗？试说明理由；
    (3)、解决问题：在图（3）中，是各边相等，各内角也相等的正五边形ABCDE，请你只用无刻度的直尺画出图中BC边的垂直平分线．

    查看试题解析