河北省2016-2017学年七年级下学期数学期末考试试卷
试卷更新日期:2017-09-26 类型:期末考试
一、选择题
-
1. 4的平方根是( )A、±2 B、2 C、﹣2 D、±2. 下列命题中,是真命题的是( )A、一个角的余角大于这个角 B、邻补角一定互补 C、相等的角是对顶角 D、有且只有一条直线与已知直线垂直3. 下列说法:①带根号的数是无理数;②不含根号的数一定是有理数;③无理数是开方开不尽的数;④无限不循环小数是无理数;⑤π是无理数,其中正确的有( )A、4个 B、3个 C、2个 D、1个4. 如果点P(a﹣3,a)在x轴上,则点P的坐标是( )A、(3,0) B、(0,3) C、(﹣3,0) D、(0,﹣3)5. 在图中,∠1和∠2是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 6. 下列调查中,适宜采用全面调查(普查)方式的是( )A、对一批圆珠笔使用寿命的调查 B、对全国九年级学生身高现状的调查 C、对某品牌烟花爆竹燃放安全的调查 D、对一枚用于发射卫星的运载火箭各零部件的检查7. 不等式2x﹣3≤1的解集在数轴上表示正确的是( )A、
6. 下列调查中,适宜采用全面调查(普查)方式的是( )A、对一批圆珠笔使用寿命的调查 B、对全国九年级学生身高现状的调查 C、对某品牌烟花爆竹燃放安全的调查 D、对一枚用于发射卫星的运载火箭各零部件的检查7. 不等式2x﹣3≤1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地抽查了n人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这n人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是( )A、 B、 C、 D、
8. 为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地抽查了n人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这n人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是( )A、 B、 C、 D、二、填空题
-
9. 如果 的平方根是±3,则 = .10. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3= .
 11. 关于x的方程组 的解是 ,则|m﹣n|的值是 .12. 已知在一个样本中,50个数据分别落在5个组内,第一,二,三,四,五组数据的个数分别是2,8,15,20,5,则第四组频数为 .13. 足球比赛中,胜一场可以积3分,平一场可以积1分,负一场得0分,某足球队最后的积分是20分,这个足球队获胜的场次最多是场.14. 若不等式组 的整数解共有三个,则a的取值范围是 .15.
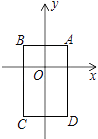
11. 关于x的方程组 的解是 ,则|m﹣n|的值是 .12. 已知在一个样本中,50个数据分别落在5个组内,第一,二,三,四,五组数据的个数分别是2,8,15,20,5,则第四组频数为 .13. 足球比赛中,胜一场可以积3分,平一场可以积1分,负一场得0分,某足球队最后的积分是20分,这个足球队获胜的场次最多是场.14. 若不等式组 的整数解共有三个,则a的取值范围是 .15.如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2017个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上.则细线的另一端所在位置的点的坐标是 .
三、解答题
-
16. 计算:2 +( ﹣1)﹣ .17. ﹣12﹣(﹣2)3× .18. 解不等式组: 并把解集在数轴上表示出来.19. 如图,把△ABC向上平移4个的那位长度,再向右平移3个单位长度,得到△A′B′C′.
 (1)、在图中画出△A′B′C′;(2)、连接A′A、C′C,求四边形A′AC′C的面积.20. 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
(1)、在图中画出△A′B′C′;(2)、连接A′A、C′C,求四边形A′AC′C的面积.20. 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
证明:∵∠3=∠4( 已知 )
∴CF∥BD
∴∠5+∠CAB=180°
∵∠5=∠6( 已知 )
∴∠6+∠CAB=180°( 等式的性质 )
∴AB∥CD
∴∠2=∠EGA
∵∠1=∠2( 已知 )
∴∠1=∠EGA( 等量代换 )
∴ED∥FB .
21. 某工程队承包了全长3150米的公路施工任务,甲、乙两个组分别从东、西两端同时施工,已知甲组比乙组平均每天多施工6米,经过5天施工,两组共完成了450米.(1)、求甲、乙两个组平均每天各施工多少米?(2)、为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多施工4米,乙组平均每天比原来多施工6米,按此施工进度,能够比原来少用多少天完成任务?22. 如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点. (1)、求△ABC的面积;(2)、如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.23. 某中学积极组织学生开展课外阅读活动,为了解本校1500名学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
(1)、求△ABC的面积;(2)、如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.23. 某中学积极组织学生开展课外阅读活动,为了解本校1500名学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题: (1)、这次抽样调查的样本容量是;(2)、x= , 并将不完整的条形统计图补充完整;(3)、若满足t≥3的人数为合格,那么估计该中学每周课外阅读时间量合格人数是多少?24. 如图,已知直线l1∥l2 , l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)、这次抽样调查的样本容量是;(2)、x= , 并将不完整的条形统计图补充完整;(3)、若满足t≥3的人数为合格,那么估计该中学每周课外阅读时间量合格人数是多少?24. 如图,已知直线l1∥l2 , l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.


(1)、若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)、若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)、若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.