广西贵港市平南县2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-26 类型：期末考试

进入出卷网下载

一、选择题

1. 下列“慢行通过，注意危险，禁止行人通行，禁止非机动车通行”四个交通标志图（黑白阴影图片）中为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算结果正确的是（）

A、（a³）²=a⁶ B、（﹣3a²）²=6a⁴ C、（﹣a²）³=a⁶ D、（﹣ $\frac{1}{2}$ ab²）³= $\frac{1}{8}$ a³b⁶

查看试题解析
3. 一次课堂练习，小颖同学做了如下4道因式分解题，你认为小颖做得不够完整的一题是（）

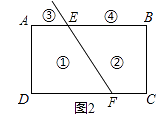
A、x²﹣y²=（x﹣y）（x+y） B、x²﹣2xy+y²=（x﹣y）² C、x²y﹣xy²=xy（x﹣y） D、x³﹣x=x（x²﹣1）

查看试题解析
4. 已知直线a、b、c相互平行，直线a与b的距离是4cm，直线b与c的距离是6cm，那么直线a与c的距离是（）

A、2cm B、5cm C、2cm或5cm D、2cm或10cm

查看试题解析
5. 一组数据3，2，2，1，2的中位数，众数及方差分别是（）

A、2，1，0.4 B、2，2，0.4 C、3，1，2 D、2，1，0.2

查看试题解析
6. 多项式x²+25添加一个单项式后可变为一个完全平方式，则添加的单项式是（）

A、5x B、﹣5x C、10x D、25x

查看试题解析
7. 若二元一次方程组 ${\begin{matrix} 2 x + 5 y = a + 2 \\ 2 x + 3 y = a \end{matrix}$ 的解x，y的和为0，则a的值为（）

A、1 B、2 C、3 D、﹣1

查看试题解析
8. 如图所示，已知CD∥AB，OE平分∠DOB，OE⊥OF，∠AOF=25°，求∠CDO的度数（）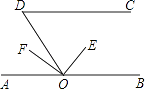

A、50° B、45° C、35° D、65°

查看试题解析
9. 如图已知∠1=∠2，∠BAD=∠BCD，则下列结论：①AB∥CD，②AD∥BC，③∠B=∠D，④∠D=∠ACB，正确的有（）

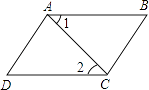A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，△COD是△AOB绕点O顺时针方向旋转38°后所得的图形，点C恰好在AB上，∠AOD=90°，那么∠BOC的度数为（）

A、12° B、14° C、24° D、30°

查看试题解析
11. 如果一组数据a₁ ， a₂ ， …a_n的平均数和方差分别是5和3，那么一组新数据a₁+2，a₂+2，a₃+2…，a_n+2平均数和方差是（）

A、5，3 B、5，4 C、7，3 D、7，5

查看试题解析
12. 哥哥与弟弟的年龄和是18岁，弟弟对哥哥说：“当我的年龄是你现在年龄的时候，你就是18岁”．如果现在弟弟的年龄是x岁，哥哥的年龄是y岁，下列方程组正确的是（）

A、 ${\begin{matrix} x = y - 18 \\ y - x = 18 - y \end{matrix}$ B、 ${\begin{matrix} y - x = 18 \\ x - y = y + 18 \end{matrix}$ C、 ${\begin{matrix} x + y = 18 \\ y - x = 18 + y \end{matrix}$ D、 ${\begin{matrix} y = 18 - x \\ 18 - y = y - x \end{matrix}$

查看试题解析

二、填空题

13. 计算（a²）⁴•（﹣a）³= ．

查看试题解析
14. 写出一个二元一次方程组，使它的解为 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ ．等．

查看试题解析
15. 某校规定学生的数学期评成绩满分为100分，其中段考成绩占40%，期考成绩占60%，小明的段考成绩是80分，数学期评成绩是86分，则小明的数学期末考试成绩是分．

查看试题解析
16. 已知a+ $\frac{1}{a}$ =4，则（a﹣ $\frac{1}{a}$ ）²= ．

查看试题解析
17. 如果一个角的两边和另外一个角的两边分别平行，其中一个角是30°，则另外一个角的度数是．

查看试题解析
18. 如图所示，将一张长方形的纸片连续对折，对折时每次折痕与上次的折痕保持平行，对折一次得到一条折痕（图中虚线），对折二次得到的三条折痕，对折三次得到7条折痕，那么对折2017次后可以得到条折痕．

查看试题解析

三、解答题

19. 因式分解：x³﹣2x²+x．

查看试题解析
20. 计算：2017²﹣2016×2018．

查看试题解析
21. 解方程组 ${\begin{matrix} x + 3 y = 9 \\ (4 y - 1) (x + 2) = 4 x y \end{matrix}$ ．

查看试题解析
22. 计算：﹣2a（3a²﹣a+3）+6a（a﹣2）² ．

查看试题解析
23. 顶点在网格交点的多边形叫做格点多边形，如图，在一个9×9的正方形网格中有一个格点△ABC设网格中小正方形的边长为1个单位长度．

(1)、在网格中画出△ABC向上平移4个单位后得到的△A₁B₁C₁；

(2)、在网格中画出△ABC绕点A逆时针旋转90°后得到的△AB₂C₂；．

查看试题解析
24. 某校九年级进行立定跳远训练，以下是刘明和张晓同学六次的训练成绩（单位：m）
刘明：2.54，2.48，2.50，2.48，2.54，2.52
张晓：2.50，2.42，2.52，2.56，2.48，2.58

(1)、填空：李明的平均成绩是．张晓的平均成绩是．

(2)、分别计算两人的六次成绩的方差，哪个人的成绩更稳定？

(3)、若预知参加年级的比赛能跳过2.55米就可能得冠军，应选哪个同学参加？请说明理由．

查看试题解析
25. 在日常生活中我们经常用到密码，如取款、上网购物需要密码，有一种用因式分解法产生密码，方便记忆，其原理是：将一个多项式因式分解：例如x⁴﹣y⁴=（x²+y²）（x+y）（x﹣y），当x=8，y=9时，x²+y²=145，x+y=17，x﹣y=4则可以得到密码是145174，1741454…，等等，根据上述方法
当x=32，y=12时，对于多项式x²y﹣y³分解因式后可以形成哪些数字密码？

查看试题解析
26. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．

(1)、CD与EF平行吗？请说明理由．

(2)、如果∠1=∠2，且∠ACB=110°，求∠3的度数．

查看试题解析
27. 某班将举行“防溺水安全知识竞赛”活动，班主任安排班长购买奖品，下面是班长买回奖品时与班主任的对话情况：
班长：买了两种不同的奖品共50件，单价分别为3元和5元，我领了200元，现在找回35元
班主任：你肯定搞错了！
班长：哦！我把自己口袋里的15元一起当作找回的钱款了．
班主任：这就对了！
请根据上面的信息，解决下列问题：

(1)、计算两种奖品各买了多少件？

(2)、请你解释：班长为什么不可能找回35元？

查看试题解析
28. 如图1，E是直线AB，CD内部一点，AB∥CD，连接EA，ED．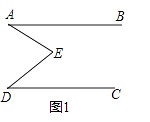

(1)、探究猜想：
①若∠A=35°，∠D=30°，则∠AED等于多少度？
②若∠A=48°，∠D=32°，则∠AED等于多少度？
③猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．

(2)、拓展应用：
如图2，射线EF与长方形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的4个区域（不含边界，其中区域③、④位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系（不要求写出证明过程）

查看试题解析