广东省广州市荔湾区2016-2017学年七年级下学期数学期末考试试卷

试卷更新日期：2017-09-26 类型：期末考试

进入出卷网下载

一、选择题

1. 在﹣2， $\sqrt{4}$ ， $\sqrt{2}$ ，3.14这4个数中，无理数是（）

A、﹣2 B、 $\sqrt{4}$ C、 $\sqrt{2}$ D、3.14

查看试题解析
2. 下列各点中，在第二象限的点是（）

A、（﹣1，4） B、（1，﹣4） C、（﹣1，﹣4） D、（1，4）

查看试题解析
3. 如图，已知∠2=100°，要使AB∥CD，则须具备另一个条件（）

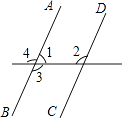A、∠1=100° B、∠3=80° C、∠4=80° D、∠4=100°

查看试题解析
4. 下列二元一次方程组的解为 ${\begin{matrix} x = 2 \\ y = - 2 \end{matrix}$ 的是（）

A、 ${\begin{matrix} x + y = 0 \\ x - y = 2 \end{matrix}$ B、 ${\begin{matrix} x + y = 0 \\ x - y = - 2 \end{matrix}$ C、 ${\begin{matrix} x + y = 0 \\ x - y = 4 \end{matrix}$ D、 ${\begin{matrix} x + y = 0 \\ x - y = - 4 \end{matrix}$

查看试题解析
5. 已知a＜b，则下列四个不等式中，不正确的是（　　）

A、a﹣2＜b﹣2 B、﹣2a＜﹣2b C、2a＜2b D、a+2＜b+2

查看试题解析
6. 以下问题，不适合使用全面调查的是（）

A、对旅客上飞机前的安检 B、航天飞机升空前的安全检查 C、了解全班学生的体重 D、了解广州市中学生每周使用手机所用的时间

查看试题解析
7. 如图，把周长为10的△ABC沿BC方向平移1个单位得到△DFE，则四边形ABFD的周长为（）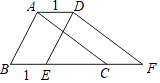

A、14 B、12 C、10 D、8

查看试题解析
8. 二元一次方程x+2y=5，若x=﹣1，则y的值为（）

A、2 B、3 C、4 D、5

查看试题解析
9. 小米家位于公园的正东100米处，从小米家出发向北走250米就到小华家，若选取小华家为原点，分别以正东，正北方向为x轴，y轴正方向建议平面直角坐标系，则公园的坐标是（）

A、（﹣250，﹣100） B、（100，250） C、（﹣100，﹣250） D、（250，100）

查看试题解析
10. 在频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其它10个小长方形面积的和的 $\frac{1}{4}$ ，且数据有160个，则中间一组的频数为（）

A、32 B、0.2 C、40 D、0.25

查看试题解析

二、填空题

11. 若P（4，﹣3），则点P到x轴的距离是．

查看试题解析
12. 如图，直线AB，CD相交于O，OE⊥AB，O为垂足，∠COE=34°，则∠BOD=度．

查看试题解析
13. 计算：|2﹣ $\sqrt{5}$ |+ $\sqrt[3]{125}$ ﹣ $\sqrt{5}$ = ．

查看试题解析
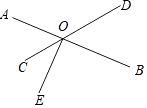14. 当x=时，3（x﹣1）的值不小于9．

查看试题解析
15. 如图，在平面直角坐标系中，一动点从原点O出发，按向上，向右，向下，向右的方向不断地移动，每次移动一个单位，得到点A₁（0，1），A₂（1，1），A₃（1，0），A₄（2，0），…那么点A₂₀₁₇的坐标为．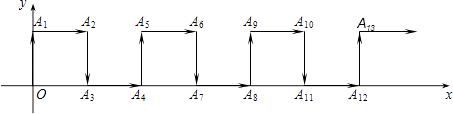

查看试题解析

三、解答题

16. 解不等式组 ${\begin{matrix} 3 x - 1 > x - 3 ① \\ x + 7 > 5 x - 1 ② \end{matrix}$ ，并把解集表示在数轴上．[注意有①②]

查看试题解析
17. 解下列方程组：(1)(2)

(1)、 ${\begin{matrix} 6 x + y = 9 ① \\ 2 x - y = - 1 ② \end{matrix}$ ；

(2)、 ${\begin{matrix} 2 x + y = - 5 ① \\ x = y - 1 ② \end{matrix}$ ．

查看试题解析
18. 如图所示，小方格边长为1个单位，

(1)、请写出△ABC各点的坐标．

(2)、求出S_△_ABC ．

(3)、若把△ABC向上平移2个单位，再向右平移2个单位△A′B′C′，在图中画出△A′B′C′．

查看试题解析
19. 某品牌的共享自行车企业为了解工作日期间地铁站附近的自行车使用情况，做到精确投放，于星期二当天对荔湾区A、B、C三个地铁站该品牌自行车后使用量进行了统计，绘制如图1和图2所示的统计图，根据图中信息解答下列问题：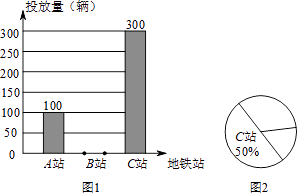

(1)、该品牌自行车当天在该三个地铁站区域投放了自行车辆．

(2)、请补全图1中的条形统计图；求出地铁A站在图2中所对应的圆心角的度数．

(3)、按统计情况，若该品牌车计划在这些区域再投放1200辆，估计在地铁B站应投入多少辆．

查看试题解析
20. 已知：如图，∠AGB=∠EHF，∠C=∠D．

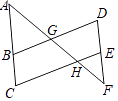(1)、求证：BC∥DE．

(2)、求证：∠A=∠F．

查看试题解析
21. 为了加强对校内外安全监控，创建荔湾平安校园，某学校计划增加15台监控摄像设备，现有甲、乙两种型号的设备，其中每台价格，有效监控半径如表所示，经调查，购买1台甲型设备比购买1台乙型设备多150元，购买2台甲型设备比购买3台乙型设备少400元．

甲型
乙型
价格（元/台）
a
b
有效半径（米/台）
150
100

(1)、求a、b的值．

(2)、若购买该批设备的资金不超过11000元，且两种型号的设备均要至少买一台，学校有哪几种购买方案？

(3)、在（2）问的条件下，若要求监控半径覆盖范围不低于1600米，为了节约资金，请你设计一种最省钱的购买方案．

查看试题解析
22. 如图，已知射线CD∥OA，点E、点F是OA上的动点，CE平分∠OCF，且满足∠FCA=∠FAC．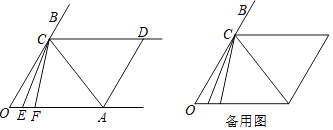

(1)、若∠O=∠ADC，判断AD与OB的位置关系，证明你的结论．

(2)、若∠O=∠ADC=60°，求∠ACE的度数．

(3)、在（2）的条件下左右平行移动AD，∠OEC和∠CAD存在怎样的数量关系？请直接写出结果（不需写证明过程）

查看试题解析

	甲型	乙型
价格（元/台）	a	b
有效半径（米/台）	150	100