浙江省温州市2020-2021学年七年级上学期数学第一次月考试卷（B卷）

试卷更新日期：2020-09-30 类型：月考试卷

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列说法中，不正确的是（）

A、0既不是正数，也不是负数 B、0不是整数 C、0的相反数是0 D、0的绝对值是0

查看试题解析
2. 在1、2、3、…99、100这100个数中，任意加上“+”或“-”，相加后的结果一定是（）

A、奇数 B、偶数 C、0 D、不确定

查看试题解析
3. 近似数8.40所表示的准确数a的范围是（）

A、8.395≤a < 8.405 B、8.30≤a≤8.50 C、8.395≤a≤8.405 D、8.400≤a≤8.405

查看试题解析
4. 两个有理数的和为负数，那么这两个数一定（）

A、都是负数 B、至少有一个是负数 C、有一个是0 D、绝对值不相等

查看试题解析
5. 如果|a|=7，|b|=5，试求a-b的值为（）

A、2 B、12 C、2和12 D、2；12；-12；-2

查看试题解析
6. 若x是有理数，则x²+1一定是（　　）

A、等于1 B、大于1 C、不小于1 D、不大于1

查看试题解析
7. 下列说法：①绝对值相等的两个数互为相反数；②绝对值等于本身的数只有正数；③不相等的两个数的绝对值不相等；④绝对值相等的两数一定相等.其中正确的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 已知a，b，c三个数在数轴上的位置如图所示，则下列各式中正确的个数为（）

①ab > 0 ②b - c > 0 ③|b - c| > c - b ④ $\frac{1}{a}$ > $\frac{1}{b}$ ⑤ $\frac{1}{b}$ > $\frac{1}{c}$

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 等边△ABC在数轴上的位置如图所示，点A，C对应的数分别为0和 - 1，若△ABC绕着顶点顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1；则翻转2020次后，点B所对应的数是（）

A、2018 B、2019 C、2020 D、2021

查看试题解析
10. 小华和小丽最近测了自己的身高，小华量得自己约1.6m，小丽测得自己的身高约为1.60m，下列关于她俩身高的说法正确的是（）

A、小华和小丽一样高 B、小华比小丽高 C、小华比小丽低 D、无法确定谁高.

查看试题解析

二、填空题（每小题4分，共24分）

11. 从数-6，1，-3，5，-2中任取二个数相乘，其积最小是.

查看试题解析
12. 若a，b互为相反数，c，d互为倒数，|m|=2，则（a+b）+3cd-m²=.

查看试题解析
13. 若有理数a，b满足|3a-1|+（b-2）²=0，则a^b的值为.

查看试题解析
14. 任取四个1至13之间的自然数，将这四个数（且每个数只能用一次）进行“＋、－、×、÷”四则运算，使其结果为24.现有四个有理数：3，4，－6，10，运用上述规则，写出一个运算：.

查看试题解析
15. 一家三口准备参加一个旅游团外出旅游，甲旅行社告知:“父母买全票，女儿半价优惠.”乙旅行社告知:“家庭旅游按团体计价，即每人均按全价的80%收费.”假定两个旅行社每人的原票价相同，均为300元，小敏一家人从中选择了较便宜的一个旅游团参加了这次旅游，他们这次旅游付出了元的旅游团费.

查看试题解析
16. 质点p从距原点1个单位的A点处向原点方向跳动，第一次从A跳动到OA的中点A₁处，第二次从A₁点跳动到OA₁的中点A₂ ，第三次从A₂跳动到OA₂的中点A₃处，如此不断地跳下去，则第10次跳动后，该质点到原点的距离为.

查看试题解析

三、解答题（17至23题分别为6，8，8，10，10，12，12分，共66分）

17. 计算:

(1)、 $\frac{2}{5}$ -|-1 $\frac{1}{2}$ |-（+2 $\frac{1}{4}$ ）-（-2.75）；

(2)、（-73）×（ $\frac{1}{2}$ -0.5）÷（- $\frac{8}{29}$ ）.

查看试题解析
18. 计算:

(1)、（ $\frac{1}{2}$ - $\frac{1}{3}$ ）÷（- $\frac{1}{6}$ ）+（-2）²×（-14）；

(2)、-1⁴-[1-（1-0.5× $\frac{1}{3}$ ）]×6.

查看试题解析
19. 在数轴上标出下列各数：0.5，-4，-2.5，2，-0.5.并把它们用“>”连接起来.

查看试题解析

20. 下表是某水站记录的潮汛期某河一周内的水位变化情况（正号表示水位比前一天上升，负号表示水位比前一天下降，上周的水位恰好达到警戒水位，单位:米）

星期	一	二	三	四	五	六	日
水位变化	+0.20	+0.81	-0.35	+0.13	+0.28	-0.36	-0.01

(1)、本周哪一天河流的水位最高，哪一天河流的水位最低，它们位于警戒水位之上还是之下，与警戒水位的距离分别是多少?

(2)、与上周末相比，本周末河流的水位是上升还是下降了?

查看试题解析

21. 王叔叔家的装修工程接近尾声，油漆工程结束了，经统计，油漆工共做50工时，用了150L油漆，已知油漆每升128元，共粉刷120m² ，在结算工钱时，有以下几种结算方案:
（ 1 ）按工时算，每6工时为300元；

（ 2 ）按油漆费用来算，油漆费用的15%为工钱；

（ 3 ）按粉刷面积来算，每6m²为132元.

请你帮王叔叔算一下，用哪种方案最省钱?

查看试题解析
22. 如图1是由若干个小圆圈堆成的一个形如正三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层.将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为 $\frac{(n (n + 1))}{2}$ .

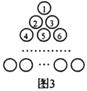
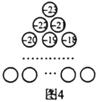
如果图1中的圆圈共有12层，

(1)、我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是；

(2)、我们自上往下，在每个圆圈中都按图4的方式填上一串连续的整数-23，-22，-21，…，求图4中所有圆圈中各数的绝对值之和.

查看试题解析
23. 观察下列等式： $\frac{1}{1 \times 2}$ =1- $\frac{1}{2}$ ， $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ - $\frac{1}{3}$ ， $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ - $\frac{1}{4}$ ；
将以上三个等式两边分别相加得： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ =1- $\frac{1}{2}$ + $\frac{1}{2}$ - $\frac{1}{3}$ + $\frac{1}{3}$ - $\frac{1}{4}$ .

(1)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ =；

(2)、计算： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2016 \times 2017}$ ；

(3)、探究并计算：
① $\frac{1}{2 \times 4}$ + $\frac{1}{4 \times 6}$ + $\frac{1}{6 \times 8}$ +…+ $\frac{1}{2016 \times 2018}$ ；

② $\frac{3}{2}$ - $\frac{5}{6}$ + $\frac{7}{12}$ - $\frac{9}{20}$ + $\frac{11}{30}$ -…+ $\frac{99}{2450}$ .

查看试题解析
24. 如果一个数等于它的不包括自身的所有因数之和，那么这个数就叫完全数.例如，6的不包括自身的所有因数为1，2，3，6=1+2+3，所以6是完全数.大约2200多年前，欧几里得提出：如果2ⁿ-1是质数，那么2^n-1·（2ⁿ-1）是一个完全数，请你根据这个结论写出6之后的下一个完全数.

查看试题解析