浙江省温州市2020-2021学年七年级上学期数学第一次月考试卷（A卷）

试卷更新日期：2020-09-30 类型：月考试卷

进入 出卷网 下载

一、选择题（每小题3分，共30分）

  • 1. 下列说法正确的是（   ）
    A、有理数分为正有理数、0、负有理数、整数和分数 B、一个有理数不是正数就是负数 C、一个有理数不是整数就是分数 D、以上说法都不正确

    查看试题解析

  • 2. 下列说法正确的个数有（   ）

    ①不带负号的数都是正数；②带负号的数不一定是负数；③0℃表示没有温度；④0既不是正数，也不是负数.

    A、0个 B、1个 C、2个 D、3个

    查看试题解析

  • 3. 按如图的程序计算，若开始输人的值为x = 3，则最后输出的结果是（   ）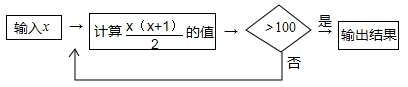

    A、6 B、21 C、156 D、231

    查看试题解析

  • 4. 如果有2020个有理数相乘所得的积为0，那么这2020个数中（   ）
    A、最多有一个数为0 B、至少有一个数为0 C、恰有一个数为0 D、均为0

    查看试题解析

  • 5. 两个有理数的和是正数，积是负数，那么这两个有理数是（   ）
    A、其中绝对值大的数是正数，另一个是负数 B、其中绝对值大的数是负数，另一个是正数 C、绝对值相等的数 D、一个数是另一个数的相反数的倒数

    查看试题解析

  • 6. 某测绘小组的技术员要测量A，B两处的高度差（A，B两处无法直接测量），他们首先选择了D，E，F，G四个中间点，并测得它们的高度差如下表：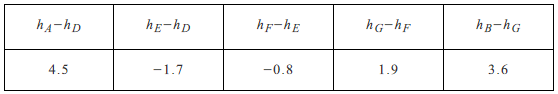

    根据以上数据，可以判断A，B之间的高度关系为（   ）

    A、B处比A处高 B、A处比B处高 C、A，B两处一样高 D、无法确定

    查看试题解析

  • 7. 若x的相反数是3，|y|=5，则x+y的值为（ ）

    A、－8 B、2 C、8或－2 D、－8或2

    查看试题解析

  • 8. 已知|a - 1| = 5，则a的值为（   ）
    A、6 B、- 4 C、6或 - 4 D、- 6或4

    查看试题解析

  • 9. a为有理数，下列说法正确的是（   ）
    A、（a+2）2为正数 B、a2+（-2）2为正数 C、a−(−12)2 为正数 D、[a+（-2）]2为正数

    查看试题解析

  • 10. 数轴上表示整数的点称为整点.某数轴的单位长度是1 cm，若在这个数轴上随意画出一条长为2020 cm的线段AB，则线段AB盖住的整点的个数是（   ）
    A、2018或2019 B、2019或2020 C、2020或2021 D、2021或2012

    查看试题解析

二、填空题（每小题4分，共24分）

  • 11. 在数轴上与表示-2的点的距离为3个单位长度的点所表示的数是.

    查看试题解析

  • 12. 一个数为-3，另一个数比-2的绝对值大1，它们的积为.

    查看试题解析

  • 13. 下面一组按规律排列的数：1，2，4，8，16，…，第2020个数应是.

    查看试题解析

  • 14. 已知|a+2|与（b-3）2互为相反数，则ab=.

    查看试题解析

  • 15. 在-20与36之间插入三个数，使这5个数中每相邻两个数之间的距离相等，则这三个数的和是.

    查看试题解析

  • 16. 小明编制了一个计算机程序，当输入任何一个有理数时，显示屏上的结果总等于所输入的这个数的绝对值与2的和.若输入-2，这时显示的结果应当是 ， 如果输入某数后，显示的结果是7，那么输入的数是.

    查看试题解析

三、解答题（17至23题分别为6，8，8，10，10，12，12分，共66分）

  • 17. 计算:
    (1)、4-（-3）×（-1）- 8×(−12)3×|-2-3| ；
    (2)、（-5）3×（- 35 ）-32÷（-2）2×（+ 54 ）.

    查看试题解析

  • 18. 每个正方体相对两个面上写的数之和等于2.

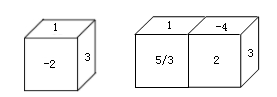    (1)、求下面正方体看不见的三个面上的数字的积.
    (2)、现将两个这样的正方体黏合放置（如图），求所有看不见的七个面上所写的数的和.

    查看试题解析

  • 19. 观察下列各等式：

    1=12

    1+3=22

    1+3+5=32

    1+3+5+7=42

    (1)、通过观察，你能推测出反映这种规律的一般结论吗?
    (2)、你能运用上述规律求1+3+5+7+…+2017的值吗?

    查看试题解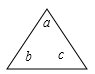析

  • 20. 若“三角” 表示适算a+b+c，“方框 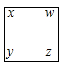表示运算x-y+z+w.

    求：表示的速算，并计算结果。

    查看试题解析

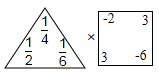  • 21. 某校举行“八荣八耻”知识竞赛，评出一等奖4人，二等奖6人，三等奖20人，学校决定给获奖学生发奖品，同一等次的奖品相同，并且只能从下表所列物品中选取一件.

    品名

    足球

    排球

    羽毛球拍

    文具盒

    相册

    钢笔

    圆规

    笔记本

    圆珠笔

    单位（元）

    30

    20

    16

    10

    8

    5

    4

    3

    2
    (1)、如果获奖等次越高，奖品的单价就越高，那么学校最少要花多少钱买奖品?
    (2)、若要求一等奖的奖品单价是二等奖的2倍，二等奖的奖品单价是三等奖的2倍，在总费用不超过200元的前提下，有几种购买方案，花费最多的一种需要多少钱?

    查看试题解析

  • 22.    
    (1)、比较下列各式的大小:

    |5|+|3||5+3|，|-5|+|-3||（-5）+（-3）|，

    |-5|+|3||（-5）+3|，|0|+|-5||0+（-5）|；

    (2)、通过（1）的比较、观察，请你猜想归纳:

    当a，b为有理数时，|a|+|b||a+b|（填入“≥”“≤”“>”或“<”）；

    (3)、根据（2）中你得出的结论，求当|x|+|-2|=|x-2|时，直接写出x的取值范围.

    查看试题解析

  • 23. 已知，如图，A，B分别为数轴上的两点，A点对应的数为-20，B点对应的数为80.
    (1)、请写出A、B两点之间相距几个单位；
    (2)、现有一只电子蚂蚁P从B点出发，以7单位/s的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3单位/s的速度向右运动，设两只电子蚂蚁在数轴上的C点相遇，你知道C点对应的数是多少吗?
    (3)、若当电子蚂蚁P从B点出发时，以7单位/s的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以3单位/s的速度也向左运动，设两只电子蚂蚁在数轴上的D点相遇，你知道D点对应的数是多少吗?

    查看试题解析