浙江省杭州市十三中2021届九年级上学期数学开学试卷
试卷更新日期:2020-09-30 类型:开学考试
一、选择题(共10小题).
-
1. 下列四种标志图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
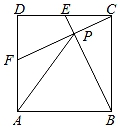
D、 2. 若 为二次根式,则m的取值范围是( )A、m<3 B、m≤3 C、m≥3 D、m>33. 下列各式中正确的是( )A、 =±6 B、 =﹣2 C、 = D、(﹣ )2=﹣74. 如图,在▱ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是( )
2. 若 为二次根式,则m的取值范围是( )A、m<3 B、m≤3 C、m≥3 D、m>33. 下列各式中正确的是( )A、 =±6 B、 =﹣2 C、 = D、(﹣ )2=﹣74. 如图,在▱ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是( ) A、 B、2 C、 D、35. 用反证法证明“四边形至少有一个角是钝角或直角”时,应先假设( )A、四边形中每个角都是锐角 B、四边形中每个角都是钝角或直角 C、四边形中有三个角是锐角 D、四边形中有三个角是钝角或直角6. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差7. 如图,一块长方形绿地的长为100m,宽为50m,在绿地中开辟两条道路后剩余绿地面积为4704m2 , 则根据题意可列出方程( )
A、 B、2 C、 D、35. 用反证法证明“四边形至少有一个角是钝角或直角”时,应先假设( )A、四边形中每个角都是锐角 B、四边形中每个角都是钝角或直角 C、四边形中有三个角是锐角 D、四边形中有三个角是钝角或直角6. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差7. 如图,一块长方形绿地的长为100m,宽为50m,在绿地中开辟两条道路后剩余绿地面积为4704m2 , 则根据题意可列出方程( )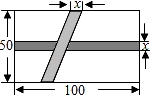 A、5000﹣150x=4704 B、5000﹣150x﹣x2=4704 C、5000﹣150x+ =4704 D、(100﹣x)(50﹣x)=47048. 如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则CD长为( )
A、5000﹣150x=4704 B、5000﹣150x﹣x2=4704 C、5000﹣150x+ =4704 D、(100﹣x)(50﹣x)=47048. 如图,将矩形ABCD的四个角向内折叠铺平,恰好拼成一个无缝隙无重叠的矩形EFGH,若EH=5,EF=12,则CD长为( ) A、13 B、 C、12 D、179. 函数y= 与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )A、
A、13 B、 C、12 D、179. 函数y= 与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )A、 B、
B、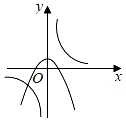 C、
C、 D、
D、 10. 如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8 ,最小值为8,则菱形ABCD的边长为( )
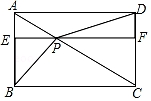
10. 如图,点P,Q分别是菱形ABCD的边AD,BC上的两个动点,若线段PQ长的最大值为8 ,最小值为8,则菱形ABCD的边长为( ) A、4 B、10 C、12 D、16
A、4 B、10 C、12 D、16二、填空题(共6小题,每小题4分)
-
11. 若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .12. 若关于x的方程x2+ax+a=0有一个根为﹣3,则a的值是.13. 已知一组数据x1 , x2 , …xn的方差是2,则另一组数据x1﹣a,x2﹣a,…,xn﹣a的方差是.14. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为.15. 若反比例函数y1= (k>0,x>0)的图象与直线y2=x﹣1在第一象限内的交点为A,点A的横坐标为m,且满足2<m<3,则k的取值范围是.16. 如图,在矩形ABCD中,点P是对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连结PB,PD.若PB=2 ,PD=5,图中阴影部分的面积和为8,则矩形ABCD的周长为.
三、解答题(本题有8小题,共66分)
-
17.(1)、计算: ×(3+ ).(2)、解方程:(x+2)2﹣3(x+2)=0.18. 某校举行了主题为“新冠肺炎防护”的知识竞赛活动,对八年级的两班学生进行了预选,其中各班前5名学生的成绩(百分制,单位:分)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级
平均分
中位数
众数
方差
八(1)
85
b
c
22.8
八(2)
a
85
85
d
(1)、直接写出表中a,b,c,d的值:a= , b= , c= , d=.(2)、根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.19. 如图,已知二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和B(3,0),与y轴交于点C.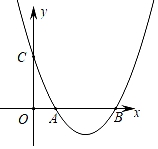 (1)、求二次函数的表达式.(2)、求二次函数图象的顶点坐标和对称轴.20. 若关于x的一元二次方程(m﹣1)x2﹣2mx+m=2有实数根.(1)、求m的取值范围;(2)、如果m是符合条件的最小整数,且一元二次方程(k+1)x2+x+k﹣3=0与方程(m﹣1)x2﹣2mx+m=2有一个相同的根,求此时k的值.21. 如图,在▱ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)、求二次函数的表达式.(2)、求二次函数图象的顶点坐标和对称轴.20. 若关于x的一元二次方程(m﹣1)x2﹣2mx+m=2有实数根.(1)、求m的取值范围;(2)、如果m是符合条件的最小整数,且一元二次方程(k+1)x2+x+k﹣3=0与方程(m﹣1)x2﹣2mx+m=2有一个相同的根,求此时k的值.21. 如图,在▱ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.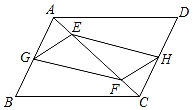 (1)、求证:四边形EGFH是平行四边形;(2)、连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.
(1)、求证:四边形EGFH是平行四边形;(2)、连接BD交AC于点O,若BD=10,AE+CF=EF,求EG的长.