河南省新乡市卫辉市2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-30 类型：期中考试

进入出卷网下载

一、选择题

1. 橡皮的单价是x元，圆珠笔的单价是橡皮的2.5倍，则圆珠笔的单价为（）

A、2.5x元 B、0.4x元 C、（x+2.5）元 D、（x-2.5）元

查看试题解析
2. 下列说法中，正确的是（）

A、正整数和负整数统称为整数； B、最小的自然数是-1 C、正分数和负分数统称为分数； D、a>-a

查看试题解析
3. 光年天文学中的距离单位，1光年大约是9500000000000km，用科学记数法表示为（）

A、 $950 \times 10^{10} km$ B、 $95 \times 10^{12} km$ C、 $9.5 \times 10^{12} km$ D、 $0.95 \times 10^{13} km$

查看试题解析
4. 在下列的代数式的写法中，表示正确的一个是（）

A、“负x的平方”记作－x² B、“y与 $1 \frac{1}{3}$ 的积”记作y $1 \frac{1}{3}$ C、“x的3倍”记作x³ D、“2 除以3b的商”记作 $\frac{2 a}{3 b}$ ；

查看试题解析
5. 下列算式中，运算结果为负数的是（）

A、 $- (- 3)$ B、 $| - 3 |$ C、 ${(- 3)}^{2}$ D、 ${(- 3)}^{3}$

查看试题解析
6. 下列说法正确的是（）

A、 $- \frac{3 xy}{5}$ 的系数是 $- 3$ B、 $2 m^{2} n$ 的次数是2次 C、 $\frac{x - 2 y}{3}$ 是多项式 D、 $x^{2} - x - 1$ 的常数项是1

查看试题解析
7. a、b、c、m都是有理数，且a＋2b＋3c＝m ， a＋b＋2c＝m ，那么b与c的关系是（　　）

A、互为相反数 B、互为倒数 C、相等 D、无法确定

查看试题解析
8. 下列由四舍五入得到的近似数说法正确的是（）

A、0.520精确到百分位 B、3.056×10⁴精确到千分位 C、6.3万精确到十分位 D、1.50精确到0.01

查看试题解析
9. 已知a、b、c三个数在数轴上对应点的位置如图所示，下列几个判断：①a<c<b；②-a<b；③a+b>0；④c-a<0中，错误的个数是（）个.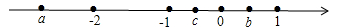

A、1 B、2 C、3 D、4

查看试题解析
10.
我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是（　　）

A、84 B、336 C、510 D、1326

查看试题解析

二、填空题

11. 把（+4）-（-6）-（+7）写成省略加号和的形式为.

查看试题解析
12. 绝对值大于2.5而小于6的整数的个数是.

查看试题解析
13. 已知m²﹣2n﹣1=0，则2m²﹣4n+5=.

查看试题解析
14. 已知数轴上有A，B两点，A，B之间的距离为3，点A对应的数为1，那么点B对应的数是.

查看试题解析
15. 三个数a、b、c的积为负数，和为正数，且 $x = \frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} + \frac{| a b |}{a b} + \frac{| a c |}{a c} + \frac{| b c |}{b c}$ ，则ax³+bx²+cx+1的值是.

查看试题解析

三、解答题

16.

(1)、 $3 \times (- 2) - 1$

(2)、 $(\frac{5}{12} + \frac{2}{3} - \frac{3}{4}) \times (- 12)$

(3)、 ${(- 2)}^{3} + (- 3) \times [{(- 4)}^{2} \times 2 \div \frac{1}{2} - 1^{4}]$

(4)、 $- 3.14 \times 35 + 6.28 \times (- 23.3) - 15.7 \times 3.68$

查看试题解析
17. 已知多项式-3x²y^m+1+x³y-3x⁴-1是五次四项式，且单项式3x²ⁿy^3-m与多项式的次数相同.

(1)、求m、n的值；

(2)、把这个多项式按x的降幂排列.

查看试题解析
18. 已知a，b均为有理数，现定义一种新的运算，规定：a#b=a²+ab-5，例如：1#2=1²+1 $\times$ 2-5=-2.求：

(1)、 $(- 3) # 6$ 的值；

(2)、 $[2 # (- \frac{3}{2})] - [(- 5) # 9]$ 的值.

查看试题解析
19. 甲、乙两个工厂今年一月份产量相同，都是a吨，三月份的产量也相同，甲厂每月产量增长的百分数（和上月相比）相同，乙厂每月产量增长的吨数（和上月相比）相同

(1)、如果上述百分数是20%，那么甲厂三月份产量是多少？（结果可以含有a）

(2)、如果上述百分数是-20%，那么乙厂二月份产量是多少？（结果可以含有a）

查看试题解析
20. 已知：a，b互为相反数，c，d互为倒数，x的绝对值是2.
求 $x^{2} - (a + b + c d) x + {(a + b)}^{2019} + {(- c d)}^{2020}$ 的值.

查看试题解析
21. 某水泥厂仓库6天内进出水泥的吨数如下（“+”表示进库，“﹣”表示出库）：+50、﹣45、﹣33、+48、﹣49、﹣36.

(1)、经过这6天，仓库里的水泥是增多还是减少了？增多或减少了多少吨？

(2)、经过这6天，仓库管理员结算发现库里还存200吨水泥，那么6天前，仓库里存有水泥多少吨？

(3)、如果进出仓库的水泥装卸费都是每吨5元，那么这6天要付多少元装卸费.

查看试题解析
22. 某公园出售的一次性使用门票，每张10元，为了吸引更多游客，新近推出购买“个人年票”的售票活动（从购买日起，可供持票者使用一年）．年票分A、B两类：
A类年票每张100元，持票者每次进入公园无需再购买门票；
B类年票每张50元，持票者进入公园时需再购买每次2元的门票．

(1)、某游客中一年进入该公园共有n次，
如果不购买年票，则一年的费用为元；
如果购买A类年票，则一年的费用为元；
如果购买B类年票，则一年的费用为元；（用含n的代数式表示）

(2)、假如某游客一年中进入该公园共有12次，选择哪种购买方式比较优惠？请通过计算说明理由．

(3)、某游客一年中进入该公园n次，他选择购买哪一类年票合算？请你帮助他决策，并说明你的理由．

查看试题解析
23. 已知式子 $M = (a + 4) x^{3} + 8 x^{2} - 2 x + 5$ 是关于x的二次多项式，且二次项系数为b，数轴上A、B两点所对应的数分别是a和b.

(1)、则a= ， b=.A、B两点之间的距离：；

(2)、有一动点P从点A出发第一次向左运动1个单位长度，然后在新的位置第二次运动，向右运动2个单位长度，在此位置第三次运动，向左运动3个单位长度…按照如此规律不断地左右运动，当运动到2019次时，求点P所对应的有理数.

(3)、在(2)的条件下，点P会不会在某次运动时恰好到达某一个位置，使点P到点B的距离是点P到点A的距离的3倍？若可能请求出此时点P的位置，若不可能请说明理由.

查看试题解析