河南省三门峡市陕州区2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-30 类型：期中考试

进入出卷网下载

一、选择题

1. $\frac{1}{2}$ 的绝对值是（）

A、–2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 武汉长江二桥是世界上第一座弧线形钢塔斜拉桥，该桥全长16800m，用科学记数法表示这个数为（）.

A、1.68×10⁴m B、16.8×10³m C、0.168×10⁴m D、1.68×10³m

查看试题解析
3. 如果收入15元记作+15元，那么支出20元记作（　　）元．

A、+5 B、+20 C、﹣5 D、﹣20

查看试题解析
4. 有理数(-1)² ， (-1)³ ， -1² ， |-1|， $- \frac{1}{- 1}$ ， $- (- 1)$ 中，其中等于1的个数是（）.

A、3个 B、4个 C、5个 D、6个

查看试题解析
5. 已知p与q互为相反数，且p≠0，那么下列关系式正确的是（）

A、p•q=1 B、 $\frac{p}{q} = 1$ C、p-q=0 D、p+q=0

查看试题解析
6. 在代数式 $\frac{a b}{3}$ ， $- \frac{2}{3} a b c$ ，0，-5，x-y， $\frac{2}{x}$ ， $\frac{1}{π}$ 中,单项式有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
7. 下列变形中，不正确的是（）

A、 $a - (b - c + d) = a - b + c - d$ B、a-b-(c-d)=a-b-c-d C、a+b-(-c-d)=a+b+c+d D、 $a + (b + c - d) = a + b + c - d$

查看试题解析
8. 如图，若数轴上的两点A，B表示的数分别为a、b，则下列结论正确的是（）

A、 $b - a > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $a + b > 0$

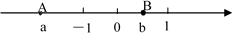查看试题解析
9. 下列说法正确的是（）

A、单项式是整式，整式也是单项式 B、 $2^{5}$ 与 $x^{5}$ 是同类项 C、单项式 $- \frac{1}{2} π x^{3} y$ 的系数是 $- \frac{1}{2} π$ ，次数是 $4$ D、 $\frac{1}{x} + 2$ 是一次二项式

查看试题解析
10. 一个多项式加上5x²﹣4x﹣3得﹣x²﹣3x，则这个多项式为（　　）

A、4x²﹣7x﹣3 B、6x²﹣x﹣3 C、﹣6x²+x+3 D、﹣6x²﹣7x﹣3

查看试题解析

二、填空题

11. 写出一个比 $- \frac{1}{2}$ 小的整数：．

查看试题解析
12. 已知甲地的海拔高度是300m，乙地的海拔高度是－50m，那么甲地比乙地高m.

查看试题解析
13. 0.0158（精确到0.001）是；1.804（精确到0.01）是.

查看试题解析
14. 若 $3 a^{m} b c^{2}$ 和 $- 2 a^{3} b^{n} c^{2}$ 是同类项，则 $m + n =$ .

查看试题解析

15. 小方利用计算机设计了一个计算程序，输入和输出的数据如下表：

输入	…	1	2	3	4	5	…
输出	…	$\frac{1}{2}$	$- \frac{2}{5}$	$\frac{3}{10}$	$- \frac{4}{17}$	$\frac{5}{26}$	…

那么，当输入数据为8时，输出的数据为．

查看试题解析

三、解答题

16. 计算：

(1)、（1﹣ $\frac{1}{6} + \frac{3}{4}$ ）×（﹣48）；

(2)、（﹣1）¹⁰×2+（﹣2）³÷4；

(3)、 $1^{4} - (1 - 0.5) \times \frac{1}{3} \times [2 - {(- 3)}^{2}]$ ；

(4)、 $- 3^{2} - \frac{1}{3} \times [{(- 5)}^{2} \times (- \frac{3}{5}) - 240 \div (- 4) \times \frac{1}{4}]$ .

查看试题解析
17.

(1)、化简： $2 (2 a^{2} + 9 b) + (- 3 a^{2} - 4 b)$

(2)、合并同类项： $3 a^{2} b + 2 a b^{2} - 5 - 3 a^{2} b - 5 a b^{2} + 2$

查看试题解析
18.

(1)、先化简再求值：3x²y﹣[2xy²﹣2（xy﹣1.5x²y）+xy]+3xy² ，其中x＝﹣3，y＝﹣2；

(2)、先化简，再求值：（2x+3y）﹣4y﹣（3x﹣2y），其中x＝﹣3，y＝2.

查看试题解析
19. 已知a、b互为相反数，c、d互为倒数，x等于﹣4的2次方，求式子（cd﹣a﹣b）x﹣ $\frac{1}{2}$ x的值.

查看试题解析
20. 若3a^mbc²和﹣2a³bⁿc²是同类项，求3m²n﹣[2mn²﹣2（m²n+2mn²）]的值.

查看试题解析

21. 某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

星期	一	二	三	四	五	六	日
增减/辆	-1	+3	-2	+4	+7	-5	-10

(1)、生产量最多的一天比生产量最少的一天多生产多少辆?

(2)、本周总的生产量是多少辆?

查看试题解析

22. 植树节甲班植树的株数比乙班多20%，乙班植树的株树比甲班的一半多10株，若乙班植树x株.

(1)、列两个不同的含x的代数式表示甲班植树的株数.

(2)、根据题意列出以x为未知数的方程.

(3)、检验乙班、甲班植树的株数是不是分别为25株和32株.

查看试题解析
23. 某商场购进一批西服，进价为每套250元，原定每套以290元的价格销售，这样每天可销售200套.如果每套比原销售价降低10元销售，则每天可多销售100套.该商场为了确定销售价格，作了如下测算，请你参加测算，并由此归纳得出结论（每套西服的利润＝每套西服的销售价﹣每套西服的进价）.

(1)、按原销售价销售，每天可获利润元.

(2)、若每套降低10元销售，每天可获利润元.

(3)、如果每套销售价降低10元，每天就多销售100套，每套销售价降低20元，每天就多销售200套.
按这种方式：

①若每套降低10x元，则每套的销售价格为元；（用代数式表示）

②若每套降低10x元，则每天可销售套西服.（用代数式表示）

③若每套降低10x元，则每天共可以获利润元.（用代数式表示）

查看试题解析