河南省南阳市唐河县2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-30 类型：期中考试

进入出卷网下载

一、选择题

1. 中国人很早开始使用负数，中国古代数学著作《九章算术》的“方程”一章，在世界数学史上首次正式引入负数．如果收入100元记作+100元．那么﹣80元表示（）

A、支出20元 B、收入20元 C、支出80元 D、收入80元

查看试题解析
2. 2019 年政府工作报告指出，我国经济运行保持在合理区间，国内生产总值增长6.6%，总量突破90万亿元。90万亿用科学记数法表示为（）

A、 $9.0 \times 10^{13}$ B、 $9.0 \times 10^{12}$ C、 $0.90 \times 10^{14}$ D、 $9.0 \times 10^{14}$

查看试题解析
3. 下列算式中，运算结果为负数的是（）

A、 $- (- 3)$ B、 $| - 3 |$ C、 ${(- 3)}^{2}$ D、 ${(- 3)}^{3}$

查看试题解析
4. 如图为某地十月份某一天的天气预报，该地这一天最高气温比最低气温高（）

A、 $- 3 {}^{\circ}C$ B、 $7 {}^{\circ}C$ C、 $3 {}^{\circ}C$ D、 $- 7 {}^{\circ}C$

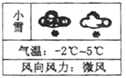查看试题解析
5. 已知a＜b，那么a-b和它的相反数的差的绝对值是（）

A、b-a B、2b-2a C、-2a D、2b

查看试题解析
6. 下列由四舍五入得到的近似数说法正确的是（）

A、0.520精确到百分位 B、3.056×10⁴精确到千分位 C、6.3万精确到十分位 D、1.50精确到0.01

查看试题解析
7. 若 $a$ 是最大的负整数， $b$ 是绝对值最小的有理数， $c$ 是倒数等于它本身的自然数，则代数式 $a^{2019} + 2020 b + c^{2019}$ 的值为（）

A、0 B、2 C、2019 D、2020

查看试题解析
8. 下列说法错误的是（）

A、 $2 x^{2} - 3 x y - 1$ 是二次三项式 B、 $- x + 1$ 不是单项式 C、 $- \frac{2}{3} π x y^{2}$ 的系数是 $- \frac{2}{3} π$ D、 $- 2^{2} x a b^{2}$ 的次数是6

查看试题解析
9. 已知a、b、c三个数在数轴上对应点的位置如图所示，下列几个判断：①a<c<b；②-a<b；③a+b>0；④c-a<0中，错误的个数是（）个.

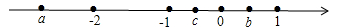A、1 B、2 C、3 D、4

查看试题解析
10. 下列语句中正确的个数是（）
① $0$ 是最小的整数:② $- 1$ 是最大的负有理数:③在数轴上到原点的距离为 $3$ 的点表示的数是 $3$ ;④有绝对值最小的有理数;⑤绝对值是本身的数是正数;⑥有理数的绝对值都是正数

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 比较大小: $- \frac{2017}{2018}$ $- \frac{2018}{2019}$ (填“ $>$ ”，“ $<$ "或“ $=$ ”)

查看试题解析
12. 果商品的原价是每件 $x$ 元，在销售时每件加价 $20$ 元，再降价 $15 %$ ，则现在每件的售价是元.

查看试题解析
13. 代数式 $y^{4} + 3 x^{2} y - 4 x^{3} y^{2} - 5 x y^{2} - 1$ 按 $x$ 的升幂排列正确的是.

查看试题解析
14. 如图，是一个简单的数值计算程序，当输入的x的值为5，则输出的结果为.

查看试题解析
15. 如图，用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案，第 $1000$ 个图案中有白色的地面砖块.

查看试题解析

三、解答题

16. 计算

(1)、 $7 \times 2.6 + 7 \times 1.5 - 4.1 \times 8$

(2)、 $- 8.125 + 7 \frac{1}{8} - 4 \frac{3}{4} + \frac{3}{4}$

(3)、 $[2 \frac{1}{2} + (\frac{3}{8} + \frac{1}{6} - \frac{3}{4}) \times 24] \div (- 5) \times {(- 1)}^{2019}$

查看试题解析
17. 把下列六个数： $+ 3 ， - 2.5 ， 0 ， - (- 2) ， - | - \frac{1}{2} | ， {(- 1)}^{2}$

(1)、分别在数轴上表示出来，并用“ $<$ ”把它们按从小到大的顺序连结起来：

(2)、填入相应的大括号内
整数集{ ……}

负分数集{ ……}

查看试题解析
18. 新学期开学，两摞规格相同准备发放的数学课本整齐地叠放在讲台上，请根据图中所给的数据信息，解答下列问题：

(1)、一本数学课本的高度是多少厘米？

(2)、讲台的高度是多少厘米？

(3)、请写出整齐叠放在桌面上的x本数学课本距离地面的高度的代数式(用含有x的代数式表示)；

(4)、若桌面上有56本同样的数学课本，整齐叠放成一摞，从中取走18本后，求余下的数学课本距离地面的高度.

查看试题解析
19. 学习有理数的乘法后，老师给同学们这样一道题目：计算：49 $\frac{24}{25}$ ×（-5），看谁算的又快又对，有两位同学的解法如下：
聪聪；原式=- $\frac{1249}{25}$ ×5=- $\frac{1249}{5}$ -249 $\frac{4}{5}$ ；

明明：原式=（49+ $\frac{24}{25}$ ）×（-5）=49×（-5）+ $\frac{24}{25}$ ×（-5）=-249 $\frac{4}{5}$ ，

(1)、对于以上两种解法，你认为谁的解法较好？

(2)、上面的解法对你有何启发，你认为还有更好的方法吗？如果有，请把它写出来；

(3)、用你认为最合适的方法计算：39 $\frac{15}{16}$ ×（-8）.

查看试题解析
20. 甲、乙两家商场以同样的价格出售同样的电器，但各自推出的优惠方案不同.甲商场规定：凡超过1000元的电器，超出的金额按90%收取;乙商场规定：凡超过500元的电器，超出的金额按95%收取. 某顾客购买的电器价格是x元.

(1)、当x=850时，该顾客应选择在商场购买比较合算;

(2)、当x>1000时，分别用代数式表示在两家商场购买电器所需付的费用;

(3)、当x=1700时，该顾客应选择哪一家商场购买比较合算?说明理由.

查看试题解析
21. 已知代数式 $a x^{3} + b x + c$ ，当 $x = 0$ 时，该代数式的值为3.

(1)、求c的值；

(2)、已知：当 $x = 1$ 时，该代数式的值为0.
①求：当 $x = - 1$ 时，该代数式的值；

②若 $a b > 0$ ， $| a | > 1$ ， $| \frac{1}{3} c d | < 1$ ，试比较a与d的大小，并说明理由.

查看试题解析
22. 某出租车驾驶员从公司出发，在东西向的路上连续接送5批客人，行驶路程记录分别为：+5，+2，﹣4，﹣3，+10（规定向东为正，向西为负，单位：千米）

(1)、接送完第5批客人后，该驾驶员在公司的什么方向？距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，则在这个过程中共耗油多少升？

(3)、若该出租车的计价标准为行驶路程不超过3千米收费10元，超过3千米的部分按每千米1.8元收费，在这过程该驾驶员共收到车费多少？

查看试题解析
23. 问题：如何快速计算1+2+3+…+n 的值呢？

(1)、探究：令s=1+2+3+…+n①，则s=n+n-1+…+2+1②
①+②得2s=(n+1)(n+1)+…+(n+1)=n $\times$ (n+1)

因此 $s =$ .

(2)、应用：
①计算： $1 + 2 + 3 + \dots + 200 =$ ；

②如图1，一串连续的整数1，2，3，4，…，自上往下排列，最上面一行有一个数，以下各行均比上一行多一个数字，若共有15行数字，则最底下一行最左边的数是；

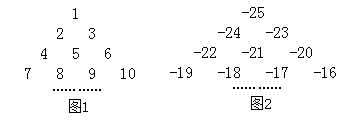
③如图2，一串连续的整数-25，-24，-23，…，按图1方式排列，共有14行数字，求图2中所有数字的和.

查看试题解析