内蒙古呼和浩特赛罕区联考2019-2020学年七年级上学期数学期中试卷
试卷更新日期:2020-09-29 类型:期中考试
一、单选题
-
1. 中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100元.那么﹣80元表示( )A、支出20元 B、收入20元 C、支出80元 D、收入80元2. 下列四个数中最小的数是A、 B、 C、0 D、53. 下列计算正确的是( )A、﹣2﹣3=1 B、a2﹣(2a﹣1)=a2﹣2a﹣1 C、(﹣7)÷ × =﹣7 D、﹣2ba2+a2b=﹣a2b4. 下列各组数中,数值相等的是( )A、﹣22和(﹣2)2 B、23和32 C、﹣33和(﹣3)3 D、(﹣3×2)2和﹣32×225. 下列说法错误的有( )
①最大的负整数是 ;
②绝对值是本身的数是正数;
③有理数分为正有理数和负有理数;
④在数轴上 与 之间的有理数是 .
A、1个 B、2个 C、3个 D、4个6. 有理数 在数轴上分别对应的点为 则下列式子结果为负数的个数是( )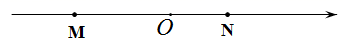
① ;② ;③ ;④ ;⑤ ;⑥ ;⑦ ;⑧
A、4个 B、5个 C、6个 D、7个7. 下列说法正确的个数是( )①有理数包括整数和分数;
②几个有理数相乘,若负因数的个数是偶数个,则积为正数;
③ 是按 的降幂排列的;
④单项式 的系数是 ,次数是 ;
⑤ 是四次四项式;
⑥一个整式不是单项式就是多项式.
A、 B、 C、 D、8. 已知a、b为有理数,且a<0,b>0,|b|<|a|,则a,b,﹣a,﹣b的大小关系是( )A、﹣b<a<b<﹣a B、﹣b<b<﹣a<a C、a<﹣b<b<﹣a D、﹣a<b<﹣b<a9. 下列说法正确的是( )A、近似数1.2× 精确到十分位 B、3.8964精确到百分位是3.90 C、近似数5.26与0.30的精确度不同 D、81.4亿用科学记数法表示为81.4×10. 下列各组单项式中,不是同类项的是A、 与 B、 与 C、 与 D、 与11. 下列结论错误的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则12. 有一批画册,若3人合看一本,则多余2本;若2人合看一本,就有9人没有,设人数为x,则列出的方程是( )A、3x+2=2x﹣9 B、 ﹣2= C、 +2= D、 +2= ﹣9二、填空题
-
13. 的倒数是 , 相反数是 .14. 已知数轴上的 点表示 .那么在数轴上与 点的距离 个长度单位的点所表示的数是 .15. 关于x方程(m+1)x|m+2|+3=0是一元一次方程,那么m= .16. 有理数 在数轴上的位置如图所示,化简; .
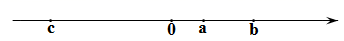 17. 一件商品每件成本 元,原来按成本增加 定出价格,现在由于库存积压减价,按原价的 出售,现售价元,每件还能盈利元.18. 已知整式 的值为 ,则 的值为
17. 一件商品每件成本 元,原来按成本增加 定出价格,现在由于库存积压减价,按原价的 出售,现售价元,每件还能盈利元.18. 已知整式 的值为 ,则 的值为三、解答题
-
19.(1)、(2)、(3)、(4)、20. 解方程:21. 先化简,再求值.(1)、 ,其中(2)、 ,其中22. 已知: 与 的和不含关于 的一次项.(1)、求 的值,并写出它们的和;(2)、请你说明不论 取什么值,这两个多项式的和总是正数的理由.23. 某自行车厂一周计划生产 辆,自行车厂平均每天生产自行车 辆,由于各种原因实际每天生产量与计划每天生产量相比有出入,下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)
星期
一
二
三
四
五
六
日
增将
(1)、根据记录可知前三天共生产自行车辆;(2)、产量最多的一天比产量最少的一天多生产辆;(3)、若该厂实行按生产的自行车数量的多少计工资(即计件工资制).如果每生产一辆自行车可得人民币 元,那么该厂工人这一周的工资总额是多少元.24. 第一车间有 人,第二车间比第一车间人数的 少 人,如果从第二车间调出 人到第一车间,求:
(1)、两个车间共有多少人?(用含 的代数式表示)(2)、调动后,第一车间的人数比第二车间多多少人?(用含 的代数式表示)25. 已知关于 的方程 和方程 的解相同,求:(1)、a的值;(2)、代数式 的值.26. 某公司在甲、乙两座仓库分别有农用车 辆和 辆,现需要调往 县 辆,调往 县 辆,已知从甲仓库调运一辆农用车到 县和 县的运费分别为 元和 元,从乙仓库调运一辆农用车到 县和 县的运费分别为 元和 元,从甲仓库调往 县农用车 辆.(1)、甲仓库调往 县农用车辆,乙仓库调往 县农用车辆、乙仓库调往B县农用车辆(用含 的代数式表示);(2)、写出公司从甲、乙两座仓库调农用车到 、 两县所需要的总运费(用含 的代数式表示);(3)、在(2)的基础上,求当总运费是 元时,从甲仓库调往 县农用车多少辆?