广西壮族自治区玉林市北流市2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-09-29 类型:期中考试
一、选择题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列函数属于二次函数的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 P(-3,-5) 关于原点对称的点的坐标是( )A、 B、 C、 D、4. 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
2. 下列函数属于二次函数的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点 P(-3,-5) 关于原点对称的点的坐标是( )A、 B、 C、 D、4. 如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( ) A、42° B、48° C、52° D、58°5. 下列关于抛物线 的说法正确的是A、抛物线开口向上 B、顶点坐标为 C、在对称轴的右侧, 随 的增大而增大 D、抛物线与 轴有两个交点6. 有一人患了流感,经过两轮传染后共有64人患了流感,则每轮传染中平均一个人传染的人数是( )A、5人 B、6人 C、7人 D、8人7. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+ C、y= (x﹣8)2+3 D、y= (x﹣4)2+38. 如图,是二次函数 的部分图象,由图象可知不等式 的解集是( )
A、42° B、48° C、52° D、58°5. 下列关于抛物线 的说法正确的是A、抛物线开口向上 B、顶点坐标为 C、在对称轴的右侧, 随 的增大而增大 D、抛物线与 轴有两个交点6. 有一人患了流感,经过两轮传染后共有64人患了流感,则每轮传染中平均一个人传染的人数是( )A、5人 B、6人 C、7人 D、8人7. 将抛物线y= x2﹣6x+21向左平移2个单位后,得到新抛物线的解析式为( )A、y= (x﹣8)2+5 B、y= (x﹣4)2+ C、y= (x﹣8)2+3 D、y= (x﹣4)2+38. 如图,是二次函数 的部分图象,由图象可知不等式 的解集是( )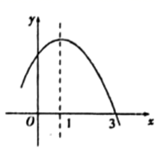 A、 B、 C、 D、 或9. 某一型号飞机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)之间的函数解析式是S=﹣1.5t2+60t,则该型号飞机着陆后滑行( )秒才能停下来.A、600 B、300 C、40 D、2010. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
A、 B、 C、 D、 或9. 某一型号飞机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)之间的函数解析式是S=﹣1.5t2+60t,则该型号飞机着陆后滑行( )秒才能停下来.A、600 B、300 C、40 D、2010. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、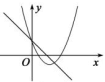 B、
B、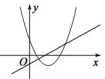 C、
C、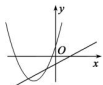 D、
D、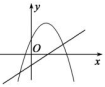 11. 如图,在 中, ,将 绕点 按逆时针方向旋转 后得到 ,则阴影部分面积为( )
11. 如图,在 中, ,将 绕点 按逆时针方向旋转 后得到 ,则阴影部分面积为( )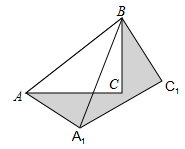 A、8 B、9 C、16 D、1812. 已知二次函数 的图象如图,分析下列四个结论:① ② ③ ④ 其中正确的结论有( )
A、8 B、9 C、16 D、1812. 已知二次函数 的图象如图,分析下列四个结论:① ② ③ ④ 其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知一元二次方程x2+kx-3=0有一个根为1,则k的值为.14. 某公司2016年的营业额为100万元,2018年的营业额为121万元,则该公司年营业额的年均增长率为.15. 的图象上有两点 , ,则 0(填“>”“<”或“=”).16. 若关于 的一元二次方程 的常数项为0,则 的值为.17. 已知 , ,则 .18. 如图,在 中, , 为 中点, , 交 于点 , 交 于点 ,则线段 , , 之间的数量关系为.

三、解答题
-
19. 解方程(1)、(2)、20. 如图, 三个顶点的坐标分别为 , , :
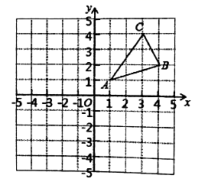
( 1 )请在图中作出 关于原点对称的图形 .
( 2 )请在图中作出 绕点 顺时针方向旋转 后得到的图形
21. 已知关于x的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、如果方程的两实根为 , ,且 ,求m的值.22.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2 , 则修建的路宽应为多少米?
 23. 一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为 2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.
23. 一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为 2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系.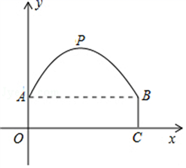 (1)、求抛物线的表达式;(2)、一辆货车高4m,宽4m,能否从该隧道内通过,为什么?24. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)、求抛物线的表达式;(2)、一辆货车高4m,宽4m,能否从该隧道内通过,为什么?24. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.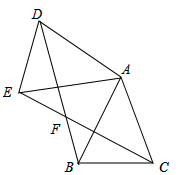 (1)、求证: ;(2)、若AB=2, ,当四边形ADFC是菱形时,求BF的长.25. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件.(1)、当销售价格上涨时,请写出每天的销售量 (件)与销售价格 (元/件)之间的函数关系式;(2)、如果要求每天的销售量不少于10件,且每件文具的利润至少为25元,问当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?26. 如图,点 在抛物线 上,且抛物线与 轴分别交于点 和点 ,与 轴交于点
(1)、求证: ;(2)、若AB=2, ,当四边形ADFC是菱形时,求BF的长.25. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售价格为25元/件时,每天的销售量为250件,每件销售价格每上涨1元,每天的销售量就减少10件.(1)、当销售价格上涨时,请写出每天的销售量 (件)与销售价格 (元/件)之间的函数关系式;(2)、如果要求每天的销售量不少于10件,且每件文具的利润至少为25元,问当销售价格定为多少时,该文具每天的销售利润最大,最大利润为多少?26. 如图,点 在抛物线 上,且抛物线与 轴分别交于点 和点 ,与 轴交于点 (1)、求抛物线的解析式.(2)、若点 为抛物线对称轴上的一个动点,求 的最小值.(3)、点 为抛物线上除点 外的一点,若 与 的面积相等,求点 的坐标。
(1)、求抛物线的解析式.(2)、若点 为抛物线对称轴上的一个动点,求 的最小值.(3)、点 为抛物线上除点 外的一点,若 与 的面积相等,求点 的坐标。