福建省南平市邵武市四中片区2019-2020学年七年级上学期数学期中试卷

试卷更新日期：2020-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. ﹣6的相反数是（　　）

A、﹣6 B、﹣ $\frac{1}{6}$ C、6 D、 $\frac{1}{6}$

查看试题解析
2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000，这个数用科学记数法表示（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、4.4×10¹⁰

查看试题解析
3. 下列各组代数式中，是同类项的是（）

A、5x²y与 $\frac{1}{5}$ xy B、﹣5x²y与 $\frac{1}{5}$ yx² C、5ax²与 $\frac{1}{5}$ yx² D、8³与x³

查看试题解析
4. 下列计算正确的是（）

A、2ab+（-2ab）=ab B、a³-a²=a C、a+a²=a³ D、a+2a=3a

查看试题解析
5. 下列交换加数的位置的变形中，正确的是（）

A、1-4+5-4=1-4+4-5 B、 $- \frac{1}{3} + \frac{3}{4} - \frac{1}{6} - \frac{1}{4} = \frac{1}{4} + \frac{3}{4} - \frac{1}{3} - \frac{1}{6}$ C、1-2+3-4=2-1+4-3 D、4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7

查看试题解析
6. 下列去括号正确的是 $($ $)$

A、 $3 x + (5 - 2 x) = 3 x + 5 + 2 x$ B、 $- (x - 6) = - x - 6$ C、 $7 x - (x + 1) = 7 x - x - 1$ D、 $3 (x + 8) = 3 x + 8$

查看试题解析
7. 如图，若A是实数a在数轴上对应的点，则关于a，－a，1的大小关系表示正确的是（）

A、a＜1＜－a B、a＜－a＜1 C、1＜－a＜a D、－a＜a＜1

查看试题解析
8. 下列根据等式的性质变形正确的是（）

A、若3x+2＝2x﹣2，则x＝0 B、若 $\frac{1}{2}$ x＝2，则x＝1 C、若x＝3，则x²＝3x D、若 $\frac{2 x + 1}{3}$ ﹣1＝x，则2x+1﹣1＝3x

查看试题解析
9. 用四舍五入法得到a的近似数为4.60，则这个数a的范围是（）

A、 $4.60 \leq a \leq 4.64$ B、 $4.55 \leq a \leq 4.65$ C、 $4.595 \leq a < 4.605$ D、 $4.595 < a < 4.605$

查看试题解析
10. 观察下列等式：7¹＝7，7²＝49，7³＝343，7⁴＝2 401，7⁵＝16 807，7⁶＝117 649，…，那么：7¹＋7²＋7³＋…＋7^{2 016}的末位数字是（）

A、9 B、7 C、6 D、0

查看试题解析

二、填空题

11. ﹣3的倒数是 ﹣3的绝对值是

查看试题解析
12. $- \frac{a^{2} b}{3}$ 系数是，多项式 $2 b + \frac{1}{4} a b^{2} - 5 a b - 1$ 的次数为

查看试题解析
13. 用四舍五入法取近似数， 2.4567≈（精确到0.001位），18042000≈（精确到万位）

查看试题解析
14. 已知xⁿy²和 $\frac{1}{2}$ x²y^m-1是同类项，则m= ， n=

查看试题解析
15. 写出一个解为－3的一元一次方程

查看试题解析
16. 一只青蛙，从A点开始在一条直线上跳着玩，第一次向右跳1厘米，第二次向左跳2厘米，第三向右次跳3厘米，第四向左跳4厘米，…依此下去．如果第2019次跳完后，请问青蛙落的位置到A点的距离是厘米

查看试题解析

三、解答题

17. 有理数计算题：
① $25 + (- 7.3) + (- 13) + 7.3$

② $(- \frac{3}{4} - \frac{5}{8} + \frac{9}{12}) \times (- 24)$

③ $(- 3) + \frac{3}{4} \times \frac{4}{3} \times (- 15)$

④ $- 2^{4} - {(- 4)}^{2} \times (- 1) + {(- 3)}^{2}$

⑤－6ab+ba+8ab

⑥－5a+2（3a－2）－（3a－7）

查看试题解析
18. 利用等式的性质解方程解一元一次方程：2－ $\frac{1}{4}$ x=3

查看试题解析
19. 先化简，再求值：﹣（3a²﹣4ab）+[a²﹣2（2a+2ab）]，其中a=﹣2，b=2017.

查看试题解析
20. 关于x，y的多项式6mx²＋4nxy＋2x＋2xy－x²＋y＋4不含二次项，求多项式2m²n＋10m－4n＋2－2m²n－4m＋2n的值．

查看试题解析
21. 若 ${(a + 3)}^{2} + | b - 2 | = 0$ ，求 ${(a + b)}^{2007} - {(a + b)}^{2008}$ 的值．

查看试题解析
22. 318路公交车上原有乘客（3m﹣n）人，中途下车一半乘客，又上车乘客（－2m+3n）人，问现在车上有乘客多少人？

查看试题解析
23. 有理数a，b，c在数轴上的位置如图所示，化简：|b﹣a|﹣|c﹣b|+|a+b|．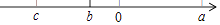

查看试题解析
24. 按如下规律摆放三角形：

(1)、图④中分别有多少个三角形？

(2)、按上述规律排列下去，第n个图形中有多少个三角形？

(3)、按上述规律排列下去，第2014个图形中有多少个三角形？

查看试题解析
25. 已知数轴上有A．B． C三点，分别表示有理数−26，−10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒。

(1)、PA= ， PC=（用含t的代数式表示）

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，当点P运动到点C时，P、Q两点运动停止，
①当P、Q两点运动停止时，求点P和点Q的距离；

②求当t为何值时P、Q两点恰好在途中相遇.

查看试题解析