广西壮族自治区崇左市天等县2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-09-29 类型:期中考试
一、选择题
-
1. 若将抛物线y=x2平移,得到新抛物线 ,则下列平移方法中,正确的是( )A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位2. 抛物线y=(x+1)2+1的顶点坐标是( )A、(1,1) B、(﹣1,1) C、(1,﹣1) D、(﹣1,﹣1)3. 下列命题中,是真命题的是( )A、等腰三角形都相似 B、等边三角形都相似 C、锐角三角形都相似 D、直角三角形都相似4. 下列函数中,当x>0时,y随x的增大而减小的是( )A、 B、 C、 D、5. 矩形的长为x,宽为y,面积为12,则y与x之间的函数关系用图象表示大致为( )A、
 B、
B、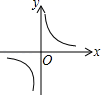 C、
C、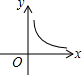 D、
D、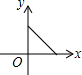 6. 如图,在 中, , ,则 ( ).
6. 如图,在 中, , ,则 ( ).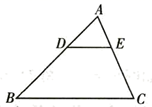 A、 B、 C、 D、7. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A、 B、 C、 D、7. 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )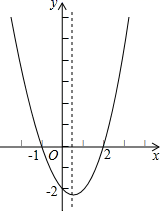 A、函数有最小值 B、对称轴是直线x= C、当x=﹣1或x=2时,y=0 D、当x>0时,y随x的增大而增大8. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、函数有最小值 B、对称轴是直线x= C、当x=﹣1或x=2时,y=0 D、当x>0时,y随x的增大而增大8. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )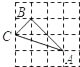 A、
A、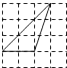 B、
B、 C、
C、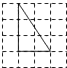 D、
D、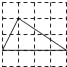 9. 根据下面表格中的对应值:
9. 根据下面表格中的对应值:x
3.23
3.24
3.25
3.26
ax2+bx+c
-0.06
-0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.2610. 已知点C是线段AB的黄金分割点(AC<BC),AB=4,则线段AC的长是( )A、 B、 C、 D、11. 如图,给出了抛物线 图象的一部分, 是抛物线与 轴的一个交点,那么抛物线与 轴的另一个交点坐标是( ).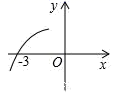 A、 B、 C、 D、12. 两个反比例函数y= 和y= 在第一象限内,点P在y= 的图象上,PC垂直于X轴于点C,交y= 的图象于点A,PD垂直于Y轴于D,交y= 的图象于点B,当点P在y= 的图象上运动时,下列结论错误的是( )
A、 B、 C、 D、12. 两个反比例函数y= 和y= 在第一象限内,点P在y= 的图象上,PC垂直于X轴于点C,交y= 的图象于点A,PD垂直于Y轴于D,交y= 的图象于点B,当点P在y= 的图象上运动时,下列结论错误的是( )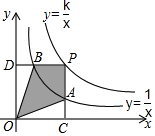 A、△ODB与△OCA的面积相等 B、当点A是PC的中点时,点B一定是PD的中点 C、只有当四边形OCPB为正方形时,四边形PAOB的面积最大 D、 =
A、△ODB与△OCA的面积相等 B、当点A是PC的中点时,点B一定是PD的中点 C、只有当四边形OCPB为正方形时,四边形PAOB的面积最大 D、 =二、填空题
-
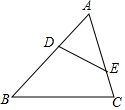
13. 若 ,则 .14. 如图,在△ABC中,点D、E分别在边AB、AC上,且DE不行于BC,添加一条件能使△ABC∽△ADE的是.
 15. 若两个三角形的相似比为2:3,则这两个三角形对应角平分线的比为 .
15. 若两个三角形的相似比为2:3,则这两个三角形对应角平分线的比为 .
16. 若A(﹣3.5,y1),B(﹣1,y2)为二次函数y=﹣(x+2)2+h的图象上的两点,则y1y2(填“>”,“=”或“<”).17. 抛物线 的顶点在y轴上,则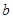 的值为. 18. 二次函数图象如图,下列结论:①abc<0;②2a﹣b=0;③对于任意实数m,都满足am2+bm≤a+b;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2.其中正确的有.(把正确的序号都填上)
的值为. 18. 二次函数图象如图,下列结论:①abc<0;②2a﹣b=0;③对于任意实数m,都满足am2+bm≤a+b;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2.其中正确的有.(把正确的序号都填上)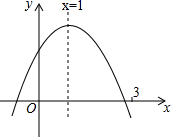
三、解答题
-
19. 已知二次函数的顶点坐标为(1,4),且其图象经过点(-2,-5),求此二次函数的解析式。20. 已知y与x成反比例,且当x=﹣2时,y=3.(1)、求y关于x的函数解析式;(2)、当x=1时,求y的值.21. 已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
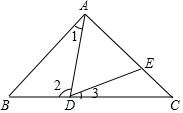 22. 已知点A(m,m+1),B(m+3,m﹣1)都在反比例函数y= 的图象上,求m的值及反比例函数的解析式.23. 如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.
22. 已知点A(m,m+1),B(m+3,m﹣1)都在反比例函数y= 的图象上,求m的值及反比例函数的解析式.23. 如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点A的坐标为(1,0),点B是点C关于该函数图象对称轴对称的点.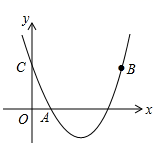 (1)、求二次函数的解析式;(2)、求点B的坐标.24. 如图,在△ABC中,∠C=90°,在AB边上取一点D,使BD=BC,过D作DE⊥AB交AC于E,AC=8,BC=6,求DE的长.
(1)、求二次函数的解析式;(2)、求点B的坐标.24. 如图,在△ABC中,∠C=90°,在AB边上取一点D,使BD=BC,过D作DE⊥AB交AC于E,AC=8,BC=6,求DE的长.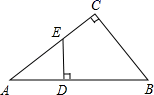 25. 已知:m , n是方程x2﹣6x+5=0的两个实数根,且m<n , 抛物线y=﹣x2+bx+c的图象经过点A(m , 0),B(0,n).
25. 已知:m , n是方程x2﹣6x+5=0的两个实数根,且m<n , 抛物线y=﹣x2+bx+c的图象经过点A(m , 0),B(0,n).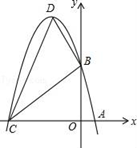 (1)、求这个抛物线的解析式;(2)、设(1)中的抛物线与x轴的另一交点为C , 抛物线的顶点为D , 试求出点C , D的坐标和△BCD的面积.26. 如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.
(1)、求这个抛物线的解析式;(2)、设(1)中的抛物线与x轴的另一交点为C , 抛物线的顶点为D , 试求出点C , D的坐标和△BCD的面积.26. 如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.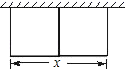 (1)、要使鸡场面积最大,鸡场的长度应为多少m?(2)、如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?
(1)、要使鸡场面积最大,鸡场的长度应为多少m?(2)、如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?比较(1)(2)的结果,你能得到什么结论?