广西壮族自治区北海市合浦县2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-09-29 类型:期中考试
一、选择题
-
1. 下列方程为一元二次方程的是( )A、ax2+bx+c=0 B、x2-2x-3 C、2x2=0 D、xy+1=02. 已知三个数为3,4,12,若再添加一个数,使这四个数能组成一个比例,那么这个数可以是( )A、1 B、2 C、3 D、43. 若面积为6cm2的平行四边形的一条边长为x(cm),这条边上的高为y(cm),则y关于x的函数表达式为( )A、xy=12 B、xy=6 C、 D、4. 方程x2=16的解是( )A、4 B、±4 C、﹣4 D、85. 反比例函数 的图象位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 如图,在ΔABC中,D、E分别是AB、AC边上的中点,连接DE,那么ΔADE与ΔABC的面积之比是( )
 A、1:16 B、1:9 C、1:4 D、1:27. 已知反比例函数 的图象在每个象限内,y都随x增大而增大,则m的值可以的是 ( )A、-1 B、0 C、1 D、28. 一元二次方程x2﹣2x+1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根9. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
A、1:16 B、1:9 C、1:4 D、1:27. 已知反比例函数 的图象在每个象限内,y都随x增大而增大,则m的值可以的是 ( )A、-1 B、0 C、1 D、28. 一元二次方程x2﹣2x+1=0的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根9. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、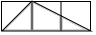 B、
B、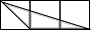 C、
C、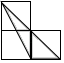 D、
D、 10. “流浪地球“一上映就获得追捧,第一天票房约8亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达29.12亿元,若把增长率记作x,则方程可以记为( )A、8(1+x)=29.12 B、8 =29.12 C、8+8(1+x)+8 =29.12 D、8+8 =29.1211. 函数 与 在同一坐标系内的图象可能是( )A、
10. “流浪地球“一上映就获得追捧,第一天票房约8亿元,以后每天票房按相同的增长率增长,三天后累计票房收入达29.12亿元,若把增长率记作x,则方程可以记为( )A、8(1+x)=29.12 B、8 =29.12 C、8+8(1+x)+8 =29.12 D、8+8 =29.1211. 函数 与 在同一坐标系内的图象可能是( )A、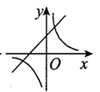 B、
B、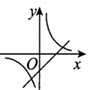 C、
C、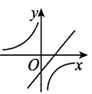 D、
D、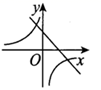 12. 如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )
12. 如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )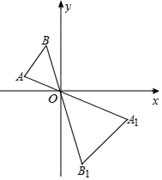 A、(2,-4) B、(1,-4) C、(-1,4) D、(-4,2)
A、(2,-4) B、(1,-4) C、(-1,4) D、(-4,2)二、填空题
-
13. 若 = ,则 = .14. 一元二次方程x2-2x-1=0的根是.15. 如图,小军在地面上合适的位置平放了一块平面镜(平面镜的高度忽略不计),刚好在平面镜中的点 处看到旗杆顶部 ,此时小军的站立点 与点 的水平距离为 ,旗杆底部 与点 的水平距离为 .若小军的眼睛距离地面的高度为 (即 ),则旗杆的高度为 .
 16. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.17. 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 = ,若点A(﹣1,0),点C( ,1),则A′C′= .
16. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.17. 如图,已知△ABC与△A′B′C′是以坐标原点O为位似中心的位似图形,且 = ,若点A(﹣1,0),点C( ,1),则A′C′= .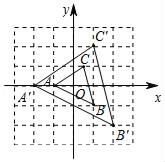 18. 如图,AD是△ABC的中线,点E在AC上,BE交AD于点F, ,则 =.
18. 如图,AD是△ABC的中线,点E在AC上,BE交AD于点F, ,则 =.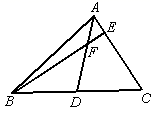
三、解答题
-
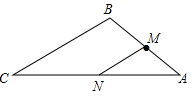
19. 用配方法解方程:4x2+8x+3=0.20. 解方程:x(x-3)-5(3-x)=0.21. 如图,已知在△ABC中,AB= ,AC=2 ,BC=3,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长.
 22. 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
22. 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.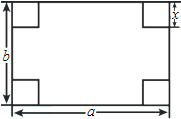 (1)、用a,b,x表示纸片剩余部分的面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.23. 如图,在△ABC中,∠ACB=90°,D为AC上的一点,DE⊥AB于点E,AC=4,BC=3.
(1)、用a,b,x表示纸片剩余部分的面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.23. 如图,在△ABC中,∠ACB=90°,D为AC上的一点,DE⊥AB于点E,AC=4,BC=3.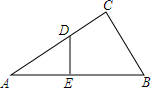 (1)、求证:△ADE∽△ABC;(2)、当DE=DC时,求AD的长.24. 如图,一次函数y1=kx+b(k≠0)和反比例函数 的图象相交于点A(﹣4,2),B(n,﹣4)
(1)、求证:△ADE∽△ABC;(2)、当DE=DC时,求AD的长.24. 如图,一次函数y1=kx+b(k≠0)和反比例函数 的图象相交于点A(﹣4,2),B(n,﹣4)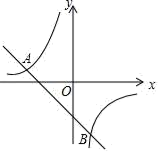 (1)、求一次函数和反比例函数的表达式;(2)、观察图象,直接写出不等式y1<y2的解集.25. 已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.
(1)、求一次函数和反比例函数的表达式;(2)、观察图象,直接写出不等式y1<y2的解集.25. 已知如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于A、B两点(OA<OB),且OA、OB的长分别是一元二次方程x2-18x+72=0的两根,点D为线段OB的中点,过点D作AB的垂线与线段AB相交于点C.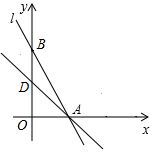 (1)、求A、B两点的坐标;(2)、求过点C的反比例函数解析式;(3)、已知点P在直线AD上,在平面内是否存在点Q,使以A、O、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q坐标;若不存在,请说明理由.26. 如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)、求A、B两点的坐标;(2)、求过点C的反比例函数解析式;(3)、已知点P在直线AD上,在平面内是否存在点Q,使以A、O、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q坐标;若不存在,请说明理由.26. 如图,在△ABC中,AD是BC边上的中线,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.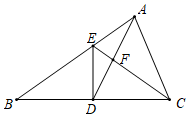 (1)、求证:△ABC∽△FCD;(2)、过点A作AM⊥BC于点M,求DE:AM的值;(3)、若S△FCD=5,BC=10,求DE的长.
(1)、求证:△ABC∽△FCD;(2)、过点A作AM⊥BC于点M,求DE:AM的值;(3)、若S△FCD=5,BC=10,求DE的长.