广西壮族自治区玉林市陆川县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-09-29 类型:期中考试
一、选择题
-
1. 通常把自行车的车身设计为三角架结构,这是因为三角形具有( )A、对称性 B、稳定性 C、全等性 D、以上说法都正确2. 下列各组数中,能作为一个三角形三边边长的是( )
A、1,1,2 B、1,2,4 C、2,3,4 D、2,3,53. 若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形"有( )对。 A、1 B、3 C、4 D、54. 下列说法:
A、1 B、3 C、4 D、54. 下列说法:①全等三角形的形状相同、大小相等②全等三角形的面积相等③周长相等的两个三角形全等④全等三角形的对应边相等、对应角相等其中正确的说法为( )
A、②③④ B、①②③ C、①②④ D、①②③④5. 一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )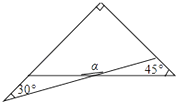 A、165° B、120° C、150° D、135°6. 下列四组条件中,可以判定 与 全等的是( )A、 B、 C、 D、7. 下列计算正确的是( )A、 B、 C、 D、8. 若 ,则A为( )A、2ab B、-2ab C、4ab D、-4ab9. 已知(x-m)(x+n)=x2-3x-4,则m-n的值为( )A、1 B、-3 C、-2 D、310. 下列因式分解正解的是( )A、 B、 C、 D、11. 如图所示,点 分别是 平分线上的点, 于点 , 于点 , 于点 ,下列结论错误的是( )
A、165° B、120° C、150° D、135°6. 下列四组条件中,可以判定 与 全等的是( )A、 B、 C、 D、7. 下列计算正确的是( )A、 B、 C、 D、8. 若 ,则A为( )A、2ab B、-2ab C、4ab D、-4ab9. 已知(x-m)(x+n)=x2-3x-4,则m-n的值为( )A、1 B、-3 C、-2 D、310. 下列因式分解正解的是( )A、 B、 C、 D、11. 如图所示,点 分别是 平分线上的点, 于点 , 于点 , 于点 ,下列结论错误的是( ) A、 B、 C、点 是 的中点 D、图中与 互余的角有两个12. 长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )
A、 B、 C、点 是 的中点 D、图中与 互余的角有两个12. 长方形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积是( )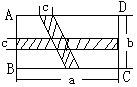 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 正n边形的一个外角是40°,则n为.14. 已知方程 的解恰好是 的两边长,则 的第三边c的取值范围是.15. 在 中,点 分别是 的中点,且 的面积等于 , .
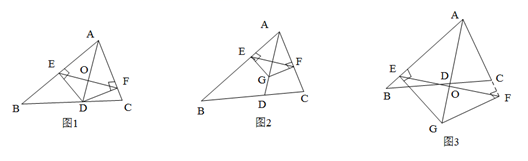
 16. 已知 ,则 =.17. 如图,在△ABC中,∠A=70°,∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为.
16. 已知 ,则 =.17. 如图,在△ABC中,∠A=70°,∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC边上点F处,若△EFC为直角三角形,则∠BDF的度数为. 18. 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=.
18. 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=.
三、解答题
-
19. 因式分解(1)、(2)、(3)、20. 化简求值(1)、 ,其中(2)、 ,其中21. 已知在△ABC中,三边长 , , 满足等式 ,试判断该三角形是什么三角形,并加以证明.22. 如图所示,已知 中, .
 (1)、作图:在 上有一点 ,连接 ,并在 的延长线上取点 ,使 ,连接 ,作 的平分线 交 于点 (用尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接 ,求证: .23. 如图所示,已知 交 于 交 于 .
(1)、作图:在 上有一点 ,连接 ,并在 的延长线上取点 ,使 ,连接 ,作 的平分线 交 于点 (用尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接 ,求证: .23. 如图所示,已知 交 于 交 于 .
求证:
(1)、 ;(2)、