广西壮族自治区南宁市马山县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2020-09-29 类型：期中考试
一、选择题
-
1. 下列各组长度的三条线段能组成三角形的是（ ）A、1cm，2cm，2cm B、1cm，1cm，2cm C、1cm，2cm，3cm D、1cm，3cm，5cm；2. 下列汽车标志不是轴对称图形的是（ ）A、
B、
C、
D、
3. 在△ABC中，∠A=40°，∠B=60°，则∠C=（ ）A、40° B、80° C、60° D、100°4. 三角形的下列线段中，能将三角形的面积分成相等两部分的是( )A、中线 B、角平分线 C、高 D、中位线5. 如图，点P是∠AOB的平分线OC上一点，PD⊥OA，垂足为D，若PD＝2，则点P到边OB的距离是（ ）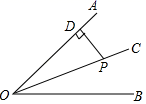
A、4 B、 C、2 D、16. 不等式 的解集为（ ）A、 B、 C、 D、7. 如图，点D在AB上，点E在AC上，AB＝AC添加下列一个条件后，还不能证明△ABE≌△ACD的是（ ）
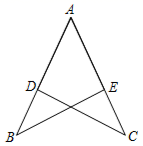A、AD＝AE B、BD＝CE C、∠B＝∠C D、BE＝CD8. 等腰三角形的一个角是80°，则它的顶角的度数是（ ）A、80° B、80°或20° C、80°或50° D、20°9. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )A、4 B、5 C、6 D、710. 已知点A（2，a）与点B（b，3）关于x轴对称，则a+b的值为（ ）A、﹣1 B、1 C、2 D、311. 如图，在△ABC中，DE是AC的垂直平分线，AE=3cm，DABD的周长为12cm，△ABC的周长为 （ ） cm.
A、15 B、16 C、17 D、1812. 如图，∠ABC和∠ACB的平分线相交于点F，过点F作DE∥BC，交AB于D，交AC于E，下列结论正确的是（ ）①BD＝CE②△BDF，△CEF都是等腰三角形③BD+CE＝DE④△ADE的周长为AB+AC.
A、①② B、③④ C、①②③ D、②③④二、填空题
-
13. 一个等腰三角形的两边长分别是3cm和6cm，则它的周长为cm．14. 在直角三角形中，两个锐角的度数比为2：3，那么较小锐角的度数是.15.
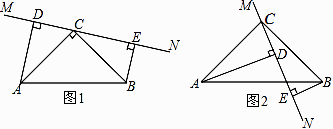
一副三角板，如图所示叠放在一起，则图中∠α的度数是
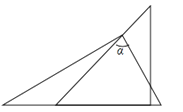16. 如图，AB＝AD，AC＝AE，请你添加一个适当的条件： ， 使得△ABC≌△ADE．
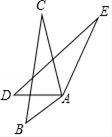17. 如图，AD是△ABC的角平分线，DE⊥AB，垂足为E，若△ABC的面积为9，DE=2，AB=5，则AC长是.
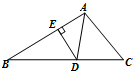18. 如图，三角形纸片ABC中，AB＝AC，∠BAC＝120°，BC＝14cm，折叠纸片，使点C和点A重合，折痕与AC，BC交于点D和点E；则折痕DE的长为.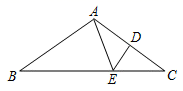
三、解答题
-
19. 计算：20. 为实施农村医疗卫生改革，计划在甲村、乙村之间建一座定点医疗站P，甲、乙两村坐落在两相交公路内，如图所示.医疗站位置必须满足下列条件：
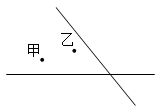
（ 1 ）使其到两条公路距离相等；
（ 2 ）到甲、乙两村的距离也相等.请你通过作图确定点P的位置.（要求尺规作图，保留痕迹，不写作法，用黑色水性笔把痕迹再描清楚）
21. 如图，在△ABC中，AD是高，AE是角平分线，∠B＝70°，∠DAE＝10°，求∠C的度数.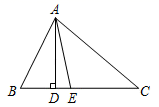
22. 如图，点A，B，C，D在同一直线上，∠M＝∠N，AM＝BN，请你添加一个条件，使得△ACM≌△BDN，并给出证明.
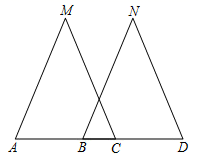(1)、你添加的条件是：.(2)、证明：23. 在如图所示的坐标系中，△ABC的三个顶点的坐标分别为A（1，2），B（4，1），C（2，﹣2）.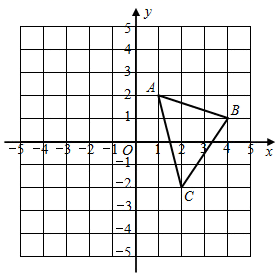
（ 1 ）请写出△ABC关于x轴对称的点A1 ， B1 ， C1的坐标；
（ 2 ）请在坐标系中作出△ABC关于y轴对称的△A2B2C2；
（ 3 ）计算△ABC的面积.
24. 如图，在△ABC中，AB＝AC，AD⊥BC于点D，BE⊥AC于点E.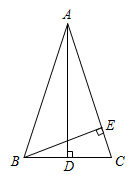
(1)、如果∠CAD＝26°，求∠ABE的度数；(2)、如果CD＝3cm，求BC的长.
