内蒙古自治区鄂尔多斯市准格尔旗2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-29 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 人字梯中间一般会设计一”拉杆”,这样做的道理是( ).
2. 人字梯中间一般会设计一”拉杆”,这样做的道理是( ).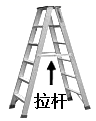 A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 一个三角形的两边长为3和8,第三边长为奇数,则第三边长为( )A、5或7 B、7或9 C、7 D、94.
A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 一个三角形的两边长为3和8,第三边长为奇数,则第三边长为( )A、5或7 B、7或9 C、7 D、94.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
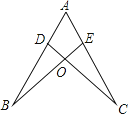 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD5. 如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A的度数等于( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD5. 如图,将纸片△ABC沿DE折叠,点A落在点F处,已知∠1+∠2=100°,则∠A的度数等于( ) A、70° B、60° C、50° D、40°6. 如图,在 中, , , , ,则 的长为( ).
A、70° B、60° C、50° D、40°6. 如图,在 中, , , , ,则 的长为( ). A、 B、 C、 D、7. 如图,三角形 中, , ,则 ( )
A、 B、 C、 D、7. 如图,三角形 中, , ,则 ( ) A、40° B、45° C、25° D、20°8. 一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )A、7 B、7或8 C、8或9 D、7或8或99. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、40° B、45° C、25° D、20°8. 一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )A、7 B、7或8 C、8或9 D、7或8或99. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( ) A、
A、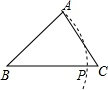 B、
B、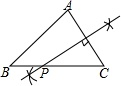 C、
C、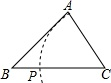 D、
D、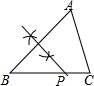 10. 如图,△ABC中,点D,E分别在BC,AC边上,E是AC的中点,BC=3BD,BE与AD相交于F,S△ABD=2,S△BFD=0.5,则四边形FDCE的面积为( )
10. 如图,△ABC中,点D,E分别在BC,AC边上,E是AC的中点,BC=3BD,BE与AD相交于F,S△ABD=2,S△BFD=0.5,则四边形FDCE的面积为( ) A、1.5 B、2.5 C、3 D、6
A、1.5 B、2.5 C、3 D、6二、填空题
-
11. 已知点 与点 关于 轴对称,则 .12. 如图,在 中, , , ,线段 , 、 两点分别在 上和 的反向延长线上移动,则当 ≌ 时, .
 13. 如图,依据尺规作图的痕迹,计算∠α=°.
13. 如图,依据尺规作图的痕迹,计算∠α=°.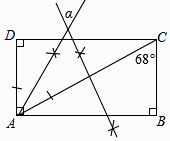 14. 如图,B、C、E三点在同一条直线上, 平分 , , 于 ,若 , ,则 的长为 .
14. 如图,B、C、E三点在同一条直线上, 平分 , , 于 ,若 , ,则 的长为 . 15. 如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是.
15. 如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是. 16. 如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.
16. 如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.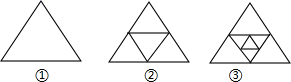
在第 个图形中有个三角形(用含 的式子表示)
三、解答题
-
17. 作图题:如图,在平面直角坐标系 中, , , .

①写出 关于 轴的对称图形 三个顶点 , , 的坐标,并画出图形;
18. 如图, 中, 是 的平分线, 交 于 , , ,求 的度数. 19. 如图所示,在 中, 是高, 、 是角平分线,它们相交于点 , , ,求 、 的度数.
19. 如图所示,在 中, 是高, 、 是角平分线,它们相交于点 , , ,求 、 的度数.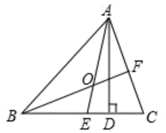 20. 点 、 、 、 在同一条直线上, , , .
20. 点 、 、 、 在同一条直线上, , , . (1)、证明: ≌ ;(2)、 和 有何关系,说明理由.21. 如图, 中, , , , .求证: .
(1)、证明: ≌ ;(2)、 和 有何关系,说明理由.21. 如图, 中, , , , .求证: . 22. 已知:在 中,点 是 的中点, 于点 , 平分 , 交 的延长线于点 , 交 于点 .求证: .
22. 已知:在 中,点 是 的中点, 于点 , 平分 , 交 的延长线于点 , 交 于点 .求证: . 23. 如图,已知 中, , 厘米, 厘米,点 为 的中点.如果点 在线段 上以每秒2厘米的速度由 点向 点运动,同时,点 在线段 上以每秒 厘米的速度由 点向 点运动,设运动时间为 (秒) .
23. 如图,已知 中, , 厘米, 厘米,点 为 的中点.如果点 在线段 上以每秒2厘米的速度由 点向 点运动,同时,点 在线段 上以每秒 厘米的速度由 点向 点运动,设运动时间为 (秒) . (1)、用含 的代数式表示 的长度;(2)、若点 、 的运动速度相等,经过1秒后, 与 是否全等,请说明理由;(3)、若点 、 的运动速度不相等,当点 的运动速度 为多少时,能够使 与 全等?24. 阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)、用含 的代数式表示 的长度;(2)、若点 、 的运动速度相等,经过1秒后, 与 是否全等,请说明理由;(3)、若点 、 的运动速度不相等,当点 的运动速度 为多少时,能够使 与 全等?24. 阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE. (1)、在图1中证明小胖的发现;
(1)、在图1中证明小胖的发现;借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)、如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;(3)、如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).