广西壮族自治区河池市凤山县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-09-29 类型:期中考试
一、选择题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点(-3,2)关于Y轴的对称点是( )A、(-3,-2) B、(3,2) C、(-3,2) D、(3,-2)3. 以下列各组线段为边,能组成三角形的是( )A、2cm,4cm,6cm B、8cm,6cm,4cm C、14cm,6cm,7cm D、2cm,3cm,6cm4. 一个多边形的内角和与外角和相等,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形5. 如图,AB∥CD,∠A=50°,∠C=30°,则∠1的大小为( )
2. 点(-3,2)关于Y轴的对称点是( )A、(-3,-2) B、(3,2) C、(-3,2) D、(3,-2)3. 以下列各组线段为边,能组成三角形的是( )A、2cm,4cm,6cm B、8cm,6cm,4cm C、14cm,6cm,7cm D、2cm,3cm,6cm4. 一个多边形的内角和与外角和相等,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形5. 如图,AB∥CD,∠A=50°,∠C=30°,则∠1的大小为( ) A、20° B、30° C、50° D、80°6. 如图,在△ABD和△ACD中,∠1=∠2,AB=AC,那么△ABD≌△ACD的依据是( )
A、20° B、30° C、50° D、80°6. 如图,在△ABD和△ACD中,∠1=∠2,AB=AC,那么△ABD≌△ACD的依据是( )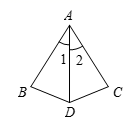 A、SAS B、AAS C、ASA D、SSS7. 如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式不一定正确的是( )
A、SAS B、AAS C、ASA D、SSS7. 如图,△ABE≌△ACD,∠1=∠2,∠B=∠C,下列等式不一定正确的是( )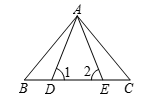 A、AB=AC B、∠BAD=∠CAE C、BE=CD D、AD=DE8. 画△ABC中BC边上的高,下面的画法中,正确的是( )A、
A、AB=AC B、∠BAD=∠CAE C、BE=CD D、AD=DE8. 画△ABC中BC边上的高,下面的画法中,正确的是( )A、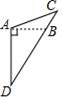 B、
B、 C、
C、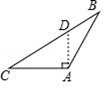 D、
D、 9. 下列说法中,错误的是( )A、全等三角形对应角相等 B、全等三角形对应边相等 C、全等三角形的面积相等 D、面积相等的两个三角形一定全等10. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )
9. 下列说法中,错误的是( )A、全等三角形对应角相等 B、全等三角形对应边相等 C、全等三角形的面积相等 D、面积相等的两个三角形一定全等10. 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点.将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于( )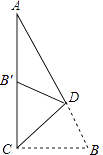 A、25° B、30° C、35° D、40°11. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、25° B、30° C、35° D、40°11. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC、AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( ) A、15 B、30 C、45 D、6012. 如图所示,在等边△ABC中,E是AC边的中点,AD是BC边上的中线,P是AD上的动点,若AD=5,则EP+CP的最小值为( )
A、15 B、30 C、45 D、6012. 如图所示,在等边△ABC中,E是AC边的中点,AD是BC边上的中线,P是AD上的动点,若AD=5,则EP+CP的最小值为( )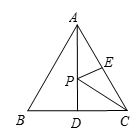 A、2 B、4 C、5 D、7
A、2 B、4 C、5 D、7二、填空题
-
13. 一个三角形的三边长分别为x,4,6,那么x的取值范围.14. 若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是 .15. 正八边形的内角和等于 .16. 将一副三角板按如图所示的方式叠放,则∠α=.
 17. 如图,△ABC中,AB = 7,AC =9,BC =5,AB的垂直平分线交AC于点D,则△BDC的周长是 .
17. 如图,△ABC中,AB = 7,AC =9,BC =5,AB的垂直平分线交AC于点D,则△BDC的周长是 .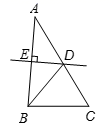 18. 如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是.
18. 如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,按此做法继续下去,第2019个等腰三角形的底角度数是.
三、解答题
-
19. 如图,已知 和A、B两点.求作点P,使P到A、B两点的距离相等,且P到 两边距离也相等(不写作法,保留作图痕迹, 写出结论).
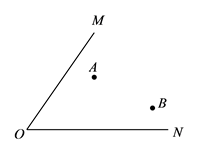 20. 如图,在△ABC中,A点坐标为(4,3),B点坐标为(-1,4),C点坐标为(-3,1).
20. 如图,在△ABC中,A点坐标为(4,3),B点坐标为(-1,4),C点坐标为(-3,1).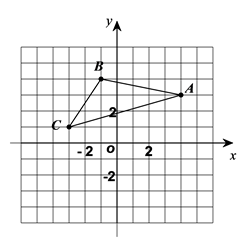 (1)、在图中画出△ABC关于x轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.(2)、在x轴上画出点P,使PA+PC最小.21. 如图,在△ABC中,∠B = 60°,∠C = 40°,AD是∠BAC的角平分线,AE是高,求∠EAD的度数.
(1)、在图中画出△ABC关于x轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标.(2)、在x轴上画出点P,使PA+PC最小.21. 如图,在△ABC中,∠B = 60°,∠C = 40°,AD是∠BAC的角平分线,AE是高,求∠EAD的度数. 22. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证: .
22. 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BE=CF.求证: .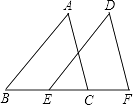 23. 如图,已知AC⊥BC,BD⊥AD,AD与BC交于点O,AC=BD.求证:△OAB是等腰三角形.
23. 如图,已知AC⊥BC,BD⊥AD,AD与BC交于点O,AC=BD.求证:△OAB是等腰三角形. 24. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5cm,DE=3cm,求BE的长.
24. 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,AD=5cm,DE=3cm,求BE的长.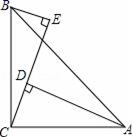 25. 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
25. 如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.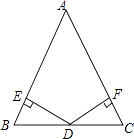 (1)、求证:DE=DF;(2)、若∠A=60°,BE=1,求△ABC的周长.26. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)、求证:DE=DF;(2)、若∠A=60°,BE=1,求△ABC的周长.26. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.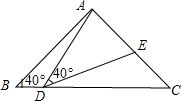 (1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.