广西壮族自治区贵港市覃塘区2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2020-09-29 类型：期中考试

进入出卷网下载

一、选择题

1. 要使分式 $\frac{2}{x + 1}$ 的值存在，则 $x$ 的取值应满足（）

A、 $x \neq 0$ B、 $x \neq 1$ C、 $x \neq - 1$ D、 $x > 0$

查看试题解析
2. 2011年3月，英国和新加坡研究人员制造出观测极限为0.00000005m的光学显微镜，这是迄今为止观测能力最强的光学显微镜.将数据0.00000005用科学记数法表示为（）

A、 0.5×10^-7 B、5×10^-8 C、5×10^-9 D、50×10^-6

查看试题解析
3. 下列式子中计算结果与 ${(- m)}^{2}$ 相同的是（）

A、 ${(m^{- 1})}^{2}$ B、 $m^{2} \times m^{- 4}$ C、 $m^{2} \div m^{4}$ D、 $m^{- 2} \div m^{- 4}$

查看试题解析
4. 已知△ABC的三个内角度数比为2：3：4，则这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
5. 如果把分式 $\frac{x + y}{x y}$ 中的x、y同时扩大为原来的2倍，那么该分式的值（　　）

A、不变 B、扩大为原来的2倍 C、缩小为原来的 $\frac{1}{2}$ D、缩小为原来的 $\frac{1}{4}$

查看试题解析
6. 到△ABC的三条边距离相等的点是△ABC的（）．

A、三条中线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条角平分线的交点

查看试题解析
7. 若 $\frac{2}{3 x^{2} - 4 x + 7}$ 的值为 $\frac{1}{4}$ ，则 $\frac{5}{6 x^{2} - 8 x - 7}$ 的值是（）

A、-1 B、1 C、 $- \frac{5}{8}$ D、 $\frac{5}{8}$

查看试题解析
8. 下列命题为真命题的是（）

A、相等的角是对顶角 B、有一个锐角和一边相等的两个直角三角形全等 C、负数一定小于它的倒数 D、面积相等的两个等腰直角三角形一定全等

查看试题解析
9. 甲、乙两单位为爱心基金分别捐款4800元、6000元，已知甲单位捐款人数比乙单位少50人，而甲单位人均捐款数比乙单位多1元.若设甲单位有x人捐款，则所列方程是（）

A、 $\frac{4800}{x} = \frac{6000}{x + 50} + 1$ B、 $\frac{4800}{x} = \frac{6000}{x - 50} + 1$ C、 $\frac{4800}{x} = \frac{6000}{x + 50} - 1$ D、 $\frac{4800}{x} = \frac{6000}{x - 50} - 1$

查看试题解析
10. 如图，在△ABC中，∠BAC=90°，点D，E分别在BC，CA边的延长线上，EH⊥BC于点H，EH与AB交于点F，则∠1与∠2的数量关系是（）

A、∠1=∠2 B、∠1与∠2互余 C、∠1与∠2互补 D、∠1+∠2=100°

查看试题解析
11. 如图，在△ABC中，点D在BC边上，DE垂直平分AC边，垂足为点E，若∠B=70°，且AB+BD=BC，则∠BAC的度数是（）

A、65° B、70° C、75° D、80°

查看试题解析
12. 如图，已知△ABC，ΔDCE都是等边三角形，且B，C，E在同一条直线上，连接BD与AC交于点M，连接AE与CD交于点N，BD与AE交于点O.给出下列五个结论：①CD∥AB；②BD=AE；③CM=CN；④AO=OE；⑤∠AOD=120°.则其中正确结论有（）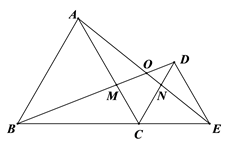

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

13. 使分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，这时x= ．

查看试题解析
14. 若代数式 ${(m + 2)}^{0} + {(m - 2)}^{- 2}$ 有意义，则m的取值范围是.

查看试题解析
15. 计算: ${(- 2)}^{- 2} + {(- 2)}^{- 1} - {(- \frac{3}{7})}^{0} =$ .

查看试题解析
16. 如图，若∠A=30°，∠B=35°，∠C=50°，则∠ADB的度数是.

查看试题解析
17. 如图，在△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于点F，若BF＝AC，则∠ABC＝度．

查看试题解析
18. 如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，若△ABC的面积为16，则图中阴影部分的面积为.

查看试题解析

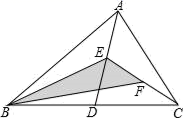
三、解答题

19. 计算:

(1)、 $(a^{2} + 5 a) \div \frac{a^{2} - 25}{a - 5}$

(2)、 $(\frac{x}{x^{2} - 2 x + 1} - \frac{x + 1}{x^{2} - x}) \div \frac{1}{x - 1}$

查看试题解析
20. 用尺规完成下列作图(只保留作图痕迹，不要求写出作法)：

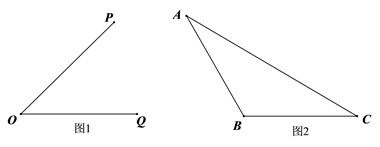(1)、如图1，求作∠POQ的平分线OM；

(2)、如图2，求作ΔABC中BC边上的高AH.

查看试题解析
21. 解下列分式方程:

(1)、 $\frac{5}{2 x} - \frac{1}{x - 3} = 0$

(2)、 $1 - \frac{3}{(x - 1) (x + 2)} = \frac{x}{x - 1}$

查看试题解析
22. 如图，CD平分∠ACB，点D是AB的中点，AE∥DC，AE交BC的延长线于点E，且∠ACE=60°，BC=8.求△ACE的周长.

查看试题解析
23. 先化简，再求值：

(1)、 $\frac{y^{2}}{x^{2} - x y} + \frac{x}{y - x}$ ，其中 $x = 2$ ， $y = - 4$ .

(2)、 $(\frac{2 x - 1}{x + 1} - x + 1) \div \frac{x - 2}{x^{2} + 2 x + 1}$ ，其中 $x = - 2$ .

查看试题解析
24. 已知：如图，点A，D，C，B在同一条直线上，AD=BCAE=BF，CE=DF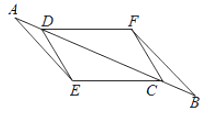
求证：

(1)、AE∥FB

(2)、DE=CF

查看试题解析
25. 某学校后勤人员到文具店给八年级学生购买考试专用文具包，该文具店规定一次性购买400个以上，可享受八折优惠.若按八年级学生实际人数每人购买一个，不能享受八折优惠，需付款1936元;若再多买88个就可享受八折优惠，并且同样只需付款1936元求该校八年级学生的总人数和文具包的价格.

查看试题解析
26. 已知△ABC是等边三角形，点D，E分别在直线BC，AC上.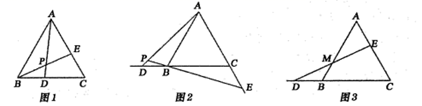

(1)、如图1，当BD=CE时，连接AD与BE交于点P，则线段AD与BE的数量关系是；∠APE的度数是；

(2)、如图2，若“BD=CE”不变，AD与EB的延长线交于点P，那么(1)中的两个结论是否仍然成立?请说明理由.

(3)、如图3，若AE=BD，连接DE与AB边交于点M，求证：点M是DE的中点.

查看试题解析