福建省三明市永安市2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-29 类型:期中考试
一、单选题
-
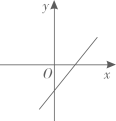
1. 在下列四个数中,是有理数的为( )A、 B、 C、 D、2. 下列各组数分别为一个三角形三边的长,其中不能构成直角三角形的一组是( )A、 , , B、 , , C、 , , D、 , ,3. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
 B、
B、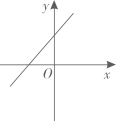 C、
C、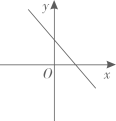 D、
D、 4. 下列各点中,在函数y=-2x+5的图象上的是( )A、(0,―5) B、(2,9) C、(–2,–9) D、(4,―3)5. 下面是一个简单的数值运算程序,当输入 的值为 时,输出的数值为( )
4. 下列各点中,在函数y=-2x+5的图象上的是( )A、(0,―5) B、(2,9) C、(–2,–9) D、(4,―3)5. 下面是一个简单的数值运算程序,当输入 的值为 时,输出的数值为( ) A、 B、 C、 或 D、6. 小丽在某动物园的大门口看到这个动物园的平面示意图(如图).若她以大门为坐标原点,向右与向上分别为x轴、y轴的正方向建立平面直角坐标系,则其他四个景点大致用坐标表示肯定错误的是( )
A、 B、 C、 或 D、6. 小丽在某动物园的大门口看到这个动物园的平面示意图(如图).若她以大门为坐标原点,向右与向上分别为x轴、y轴的正方向建立平面直角坐标系,则其他四个景点大致用坐标表示肯定错误的是( )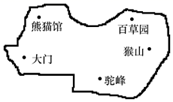 A、熊猫馆(1,4) B、猴山(6,1) C、百草园(5,-3) D、驼峰(5,-2)7. 已知一次函数y=kx+1,y随x的增大而减小,则该函数的图象一定经过( )
A、熊猫馆(1,4) B、猴山(6,1) C、百草园(5,-3) D、驼峰(5,-2)7. 已知一次函数y=kx+1,y随x的增大而减小,则该函数的图象一定经过( )
A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限8. 下列各式中属于最简二次根式的是( )A、 B、 C、 D、9. 如图,在圆柱的截面ABCD中,AB= ,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为_______. A、10 B、12 C、20 D、1410. 如图,在矩形 中, , ,动点 沿折线 从点 开始运动到点 .设运动的路程为 , 的面积为 ,那么 与 之间的函数关系的图象大致是( )
A、10 B、12 C、20 D、1410. 如图,在矩形 中, , ,动点 沿折线 从点 开始运动到点 .设运动的路程为 , 的面积为 ,那么 与 之间的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 9的平方根是 ,使分式有意义的x的取值范围是 .12. 点 关于 轴的对称点坐标为 .13. 比较大小: (填写“>”或“<”).14. 上图阴影部分是一个等腰直角三角形,则此等腰直角三角形的面积为cm2 .
 15. 若直线 平行于直线 ,且经过点 ,则b= .16. 如图,在平面直角坐标系中,已知点P(2,1),点A是x轴上的一个动点,当△PAO是等腰三角时,点A的坐标为.
15. 若直线 平行于直线 ,且经过点 ,则b= .16. 如图,在平面直角坐标系中,已知点P(2,1),点A是x轴上的一个动点,当△PAO是等腰三角时,点A的坐标为.
三、解答题
-
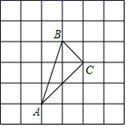
17.(1)、(2)、(3)、(4)、18. 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
 19. 如图所示的正方形网格中,每个小正方形的边长为1,格点三角形 (顶点是网格线的交点的三角形)的顶点 , 的坐标分别为 , .
19. 如图所示的正方形网格中,每个小正方形的边长为1,格点三角形 (顶点是网格线的交点的三角形)的顶点 , 的坐标分别为 , .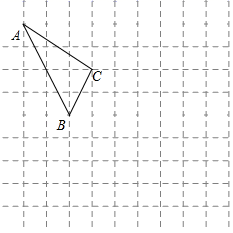 (1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、点 到 轴的距离是;(3)、请作出 关于 轴对称的 ;(4)、写出点 的坐标 .20. 已知 的立方根是 , 的算术平方根是 , 的小数部分为 .(1)、分别求出 , , 的值;(2)、求 的平方根.21. 如图,直线 与 轴相交于点 ,与 轴相交于点 .
(1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、点 到 轴的距离是;(3)、请作出 关于 轴对称的 ;(4)、写出点 的坐标 .20. 已知 的立方根是 , 的算术平方根是 , 的小数部分为 .(1)、分别求出 , , 的值;(2)、求 的平方根.21. 如图,直线 与 轴相交于点 ,与 轴相交于点 .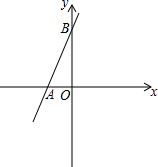 (1)、求 , 两点的坐标;(2)、过 点作直线 与 轴相交于 ,且使 ,求 的面积.22. 已知,如图, 中, , , ,以斜边 为底边作等腰三角形 ,腰 刚好满足 ,并作腰上的高 .
(1)、求 , 两点的坐标;(2)、过 点作直线 与 轴相交于 ,且使 ,求 的面积.22. 已知,如图, 中, , , ,以斜边 为底边作等腰三角形 ,腰 刚好满足 ,并作腰上的高 . (1)、求证: ;(2)、求等腰三角形的腰长 .
(1)、求证: ;(2)、求等腰三角形的腰长 .