福建省三明市大田县2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，属于无理数的是（）

A、0 B、 $- \frac{1}{2}$ C、 $π$ D、3.14

查看试题解析
2. 在平面直角坐标系中，点M（-1，1）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 以下四组数中，不是勾股数的是（）

A、8，5，7 B、5，12，13 C、20，21，29 D、3n，4n，5n（n为正整数）

查看试题解析
4. 下列等式成立的是（）

A、 $\sqrt{25} = \pm 5$ B、 $\sqrt[3]{{(- 3)}^{3}} = 3$ C、 $\sqrt{{(- 4)}^{2}} = - 4$ D、 $\pm \sqrt{0.36} = \pm 0.6$

查看试题解析
5. 过原点和点（2，3）的直线的解析式为（）

A、y＝ $\frac{3}{2}$ x B、y＝ $\frac{2}{3}$ x C、﹣y＝ $\frac{3}{2}$ x D、﹣y＝ $\frac{2}{3}$ x

查看试题解析
6. 下列说法正确的是（）

A、一个数的平方根有两个，它们互为相反数 B、一个数的立方根不是正数就是负数 C、负数没有立方根 D、如果一个数的立方根是这个数本身，那么这个数一定是-1或0或1

查看试题解析
7. 如图有一圆柱，高为8cm，底面直径为4cm，在圆柱下底面A点有一只蚂蚁，它想吃上底面与A相对的B点处的食物，需爬行的最短路程大约为(取 $π = 3$ )（）

A、10cm B、12cm C、14cm D、20cm

查看试题解析
8. 已知一次函数y=kx+b，当−3＜x＜1时，对应的y值为−1＜y＜3，则b的值是（）

A、2 B、3或0 C、3 D、2或0

查看试题解析
9. 已知坐标平面内的点A（3，2），B（1，3），C（﹣1，﹣6），D（2a，4a﹣4）中只有一点不在直线l上，则这一点是（）

A、点A B、点B C、点C D、点D

查看试题解析
10. 如图，由四个全等的直角三角形拼成的图形，设 $C E = a$ ， $H G = b$ ，则斜边BD的长是（）

A、 $a + b$ B、 $a \cdot b$ C、 $\sqrt{\frac{a^{2} + b^{2}}{2}}$ D、 $\sqrt{\frac{a^{2} - b^{2}}{2}}$

查看试题解析

二、填空题

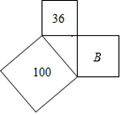
11. 在实数 $\sqrt{2}$ ，﹣1.5，π，3中，最大的实数是

查看试题解析
12. 如图，两个正方形的面积分别是100和36，则字母B所代表的正方形的面积是

查看试题解析
13. 如图，OB是边长为1的正方形的对角线，且OA＝OB，数轴上A点对应的数是：．

查看试题解析
14. 若点 $(m ， n)$ 在函数 $y = 3 x - 7$ 的图像上,则 $3 m - n$ 的值为.

查看试题解析
15. 如图，一次函数y＝kx+b的图象与x轴相交于点（﹣2，0），与y轴相交于点（0，3），则关于x的方程kx＝b的解是．

查看试题解析
16. 当m，n是正实数，且满足m+n＝mn时，就称点P（m， $\frac{m}{n}$ ）为“完美点”．已知点A（1，6）与点B的坐标满足y＝﹣x+b，且点B是“完美点”．则点B的坐标是．

查看试题解析

三、解答题

17. 根据要求解答下列各题．

(1)、求下列各式中的x的值．
① $2 x^{2} = 8$

② ${(2 - x)}^{3} = 64$

(2)、计算．
① $\sqrt{9} - \sqrt{{(- 6)}^{2}} - \sqrt[3]{- 27}$

② $\frac{\sqrt{18} - \sqrt{8}}{\sqrt{2}}$

查看试题解析
18. 已知点P（ $a - 2$ ， $2 a - 8$ ），分别根据下列条件求出点P的坐标．

(1)、点P在x轴上；

(2)、点Q的坐标为（1，5），直线PQ∥y轴．

(3)、点P到x轴、y轴的距离相等；

查看试题解析
19. 如图，在正方形网格中，每个小方格的边长都为1，△ $A B C$ 各顶点都在格点上．若点 $A$ 的坐标为（0，3），请按要求解答下列问题：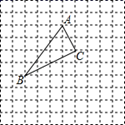

(1)、在图中建立符合条件的平面直角坐标系；

(2)、根据所建立的坐标系，写出点 $B$ 和点 $C$ 的坐标；

(3)、画出△ $A B C$ 关于 $x$ 轴的对称图形△ $A^{'} B^{'} C^{'}$ ．

查看试题解析
20. 已知： $x = \sqrt{3} + \sqrt{2}, y = \sqrt{3} - \sqrt{2}$ ，求 $\frac{x^{2} - x y + y^{2}}{x y}$

查看试题解析
21. 已知等腰三角形ABC的底边BC＝20cm，D是腰AB上一点，且CD＝16cm，BD＝12cm

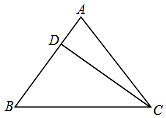(1)、请判断CD与AB的位置关系，并说明理由；

(2)、求该三角形的腰的长度．

查看试题解析
22. 阅读例题，再解答问题：
例题：请表示 $\sqrt{6}$ 的小数部分．

解：因为 $\sqrt{6}$ 的整数部分是2，将 $\sqrt{6}$ 减去其整数部分，差就是小数部分．所以 $\sqrt{6}$ 的小数部分是 $\sqrt{6}$ ﹣2．

问题：

(1)、请表示 $\sqrt[3]{9}$ 的小数部分．

(2)、已知7+ $\sqrt{13}$ ＝x+y，其中x是一个整数，且0＜y＜1，求出3x+（ $\sqrt{13}$ ﹣y）的值．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $l$ 是第一、三象限的角平分线.

(1)、由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标： $B^{'}$ 、 $C^{'}$ ；

(2)、结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点 $P (a ， b)$ 关于第一、三象限的角平分线 $l$ 的对称点 $P^{'}$ 的坐标为（不必证明）；

(3)、已知两点 $D (1 ， - 3)$ 、 $E (- 1 ， - 4)$ ，试在直线L上画出点Q，使点Q到D、E两点的距离之和最小，求QD+QE的最小值．

查看试题解析

24. 八年级（1）班张山同学利用所学函数知识，对函数y＝|x+2|﹣x﹣1进行了如下研究：

列表如下：

x		﹣5	﹣4	﹣3	﹣2	﹣1	0	1	2	3
Y		7	5	3	m	1	n	1	1	1

描点并连线（如下图）

(1)、求表格中的m、n的值；

(2)、在给出的坐标系中画出函数y＝|x+2|﹣x﹣1的图象；

(3)、一次函数y＝﹣x+3的图象与函数y＝|x+2|﹣x﹣1的图象交点的坐标为．

查看试题解析

25. 如图1：已知直线 $y = - 2 x + 2$ 与 $y$ 轴， $x$ 轴分别交于 $A$ ， $B$ 两点，以 $B$ 为直角顶点在第一象限内做等腰Rt△ $A B C$ ．

(1)、求 $A$ ， $B$ 两点的坐标；

(2)、求 $B C$ 所在直线的函数关系式；

(3)、如图2，直线 $B C$ 交 $y$ 轴于点 $D$ ，在直线 $B C$ 上存在一点 $E$ ，使 $A D$ 是△ $A B E$ 的中线，求点E的坐标．

查看试题解析