福建省福州市闽清县2019-2020学年八年级上学期数学期中试卷

试卷更新日期：2020-09-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不具有稳定性的图形是（）

A、平行四边形 B、等腰三角形 C、直角三角形 D、等边三角形

查看试题解析
2. 下列运算正确的是（）

A、a³•a⁴＝a¹² B、（a³）²＝a⁵ C、（3a²）³＝27a⁶ D、a⁶÷a³＝a²

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、5,8,14 B、3,6,11 C、4,6,10 D、2,3,4

查看试题解析
4. 若一个多边形的内角和是900°，则这个多边形的边数是（）

A、5 B、6 C、7 D、8

查看试题解析
5. 若等式 ${(a - b)}^{2} + M = {(a + b)}^{2}$ 成立，则M是（）

A、 $2 a b$ B、 $4 a b$ C、－ $4 a b$ D、－ $2 a b$

查看试题解析
6. 如图，在∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB的依据是（）

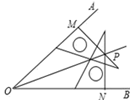A、HL B、SAS C、AAS D、SSS

查看试题解析
7. 若 $x^{2} - k x + 81$ 是一个完全平方式，则k的值为（）

A、 $\pm 9$ B、18 C、 $\pm 18$ D、 $- 18$

查看试题解析
8. 已知a、b、c是△ABC的三条边长，化简|a＋b－c|－|c－a－b|的结果为（）

A、2a＋2b－2c B、2a＋2b C、2c D、0

查看试题解析
9. 下列说法中，正确的是（）

A、等腰三角形底边上的中线就是底边的垂直平分线 B、等腰三角形的对称轴是底边上的高 C、一条线段可看做是以它的垂直平分线为对称轴的轴对称图形 D、等腰三角形的对称轴就是顶角平分线

查看试题解析
10. 如图，在2×2的方格纸中有一个以格点为顶点的△ABC，则与△ABC成轴对称且以格点为顶点三角形共有（）个.

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 点M（1，2）关于x轴对称的点的坐标为．

查看试题解析
12.
已知射线OM．以O为圆心，任意长为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，如图所示，则∠AOB= 　（度）

查看试题解析
13. 如图，△ABC中，∠ACB＝90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A＝22°，则∠ADE＝°．

查看试题解析
14. 等腰三角形一个内角的大小为50°，则其顶角的大小为度．

查看试题解析
15. 已知一个三角形的三边长分别是n+2，n+8，3n，则n的取值范围．

查看试题解析
16. 如图，在△ABC中，∠BCA＝120°，∠A＝15°，AC＝5，点M、N分别是AB、AC上动点，则CM+MN的最小值为．

查看试题解析

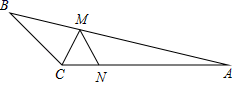
三、解答题

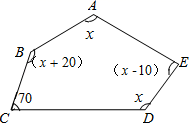
17. 计算：

(1)、（﹣3x）²（x﹣3y）

(2)、（12a³﹣6a²+3a）÷3a

查看试题解析
18. 分解因式：

(1)、a³b﹣ab；

(2)、（a﹣b）²﹣6（a﹣b）+9．

查看试题解析
19. 先化简，再求值：（2x﹣3y）²﹣（2x﹣y）（2x+y），其中x＝﹣ $\frac{1}{3}$ ，y＝ $\frac{1}{2}$ ．

查看试题解析
20. 求图形中x的值：

查看试题解析
21. 如图，在△ABC中，D是BC边的中点，且AD平分∠BAC，DE⊥AB，DF⊥AC，垂足分别是E，F，求证：△ABC是等腰三角形．

查看试题解析
22. △ABC在平面直角坐标系中的位置如图所示：

(1)、写出点A，B，C三点的坐标；

(2)、若△ABC各顶点的横坐标不变，纵坐标都乘以﹣1，请你在同一坐标系中描出对应的点A'，B'，C'，并依次连接这三点，所得的△A'B'C'与原△ABC的位置关系是什么？

(3)、在x轴上作出一点P，使得AP平分∠BAC．（保留作图痕迹，不写作法）

查看试题解析
23. 在△ABC中，BC＝a，AC＝b，AB＝c，且满足a²+b²+ $\frac{1}{2} c^{2}$ ＝ac+bc，试判定△ABC的形状，并说明理由．

查看试题解析
24. 观察等式：2+2²＝2³﹣2；2+2²+2³＝2⁴﹣2；2+2²+2³+2⁴＝2⁵﹣2……
请根据以上规律，完成下列问题：

(1)、填空：2+2²+2³+2⁴+2⁵+…+2²⁰¹⁹＝；

(2)、写出第n个等式：；

(3)、已知按一定规律排列的一组数：2⁵⁰ ， 2⁵¹ ， 2⁵² ， …2⁹⁹ ， 2¹⁰⁰ ．若2⁵⁰＝a，请用含a的式子表示这组数的和．（要求写出解答过程）

查看试题解析
25. 如图1，△ABC中，AB＝AC，∠BAC＝90°，CD平分∠ACB，BE⊥CD，垂足E在CD的延长线上.请解答下列问题：

(1)、图中与∠DBE相等的角有：；

(2)、直接写出BE和CD的数量关系；

(3)、若△ABC的形状、大小不变，直角三角形BEC变为图2中直角三角形BED，∠E＝90°，且∠EDB＝ $\frac{1}{2}$ ∠C，DE与AB相交于点F.试探究线段BE与FD的数量关系，并证明你的结论.

查看试题解析